第15页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
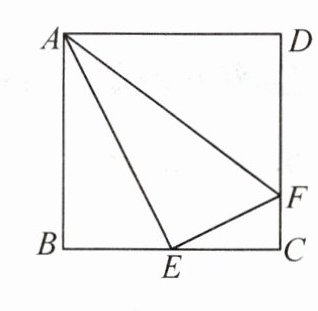
10. 人大附中校本经典题 如图,在正方形 $ ABCD $ 中, $ E $ 是 $ BC $ 的中点, $ F $ 是 $ CD $ 上一点,且 $ CF = \dfrac{1}{4}CD $,试说明: $ \angle AEF = 90^{\circ} $.

答案:
10.解:四边形ABCD为正方形,
∴AB = BC = CD = DA,∠B = ∠C = ∠D = 90°.设AB = BC = CD = DA = 4a.
∵E是BC的中点,且CF=1/4CD,
∴BE = BC = 2a,CF = a.
∴DF = 4a - a = 3a.在Rt△ABE中,由勾股定理,得AE² = AB² + BE² = 20a².同理可得,EF² = EC² + FC² = 5a²,AF² = AD² + DF² = 25a².
∵AE² + EF² = AF²,
∴△AEF为直角三角形.
∴∠AEF = 90°.
∴AB = BC = CD = DA,∠B = ∠C = ∠D = 90°.设AB = BC = CD = DA = 4a.
∵E是BC的中点,且CF=1/4CD,
∴BE = BC = 2a,CF = a.
∴DF = 4a - a = 3a.在Rt△ABE中,由勾股定理,得AE² = AB² + BE² = 20a².同理可得,EF² = EC² + FC² = 5a²,AF² = AD² + DF² = 25a².
∵AE² + EF² = AF²,
∴△AEF为直角三角形.
∴∠AEF = 90°.
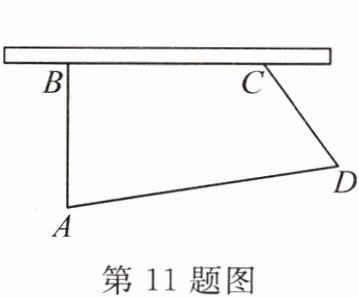
11. 如图,学校在校园围墙边缘开垦一块四边形菜地 $ ABCD $,测得 $ AB = 9 m $, $ BC = 12 m $, $ CD = 8 m $, $ AD = 17 m $,且 $ \angle ABC = 90^{\circ} $,则这块菜地的面积是(
A.$ 48 m^{2} $
B.$ 114 m^{2} $
C.$ 122 m^{2} $
D.$ 158 m^{2} $
B
)
A.$ 48 m^{2} $
B.$ 114 m^{2} $
C.$ 122 m^{2} $
D.$ 158 m^{2} $
答案:
11.B
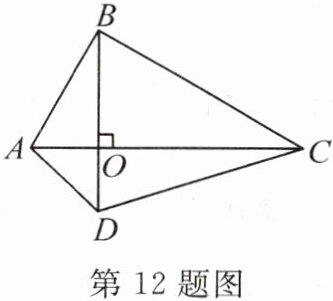
12. 对角线互相垂直的四边形叫作“垂美”四边形,现有如图所示的“垂美”四边形 $ ABCD $,对角线 $ AC,BD $ 交于点 $ O $. 若 $ AD = 2 $, $ BC = 4 $,则 $ AB^{2} + CD^{2} = $
20
.
答案:
12.20
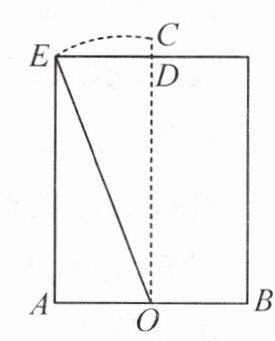
13. (教材 P21 新增复习题 T8 变式)《九章算术》卷九“勾股”中记载:“今有池方一丈,葭生其中央,出水一尺. 引葭赴岸,适与岸齐,问水深、葭长各几何?”大意:如图,水池底面的宽 $ AB = 1 $ 丈,芦苇 $ OC $ 生长在 $ AB $ 的中点 $ O $ 处,高出水面的部分 $ CD = 1 $ 尺. 将芦苇向池岸牵引,尖端达到岸边时恰好与水面平齐,即 $ OC = OE $,求水池的深度和芦苇的长度. (1 丈 $ = 10 $ 尺).
(1)求水池的深度 $ OD $.
(2)我国古代数学家刘徽在为《九章算术》作注解时,更进一步给出了这类问题的一般解法. 他的解法用现代符号语言可以表示为:若已知水池宽 $ AB = 2a $,芦苇高出水面的部分 $ CD = n(n \lt a) $,则水池的深度 $ OD (OD = b) $ 可以通过公式 $ b = \dfrac{a^{2} - n^{2}}{2n} $ 计算得到. 请说明刘徽解法的正确性.
(1)求水池的深度 $ OD $.
(2)我国古代数学家刘徽在为《九章算术》作注解时,更进一步给出了这类问题的一般解法. 他的解法用现代符号语言可以表示为:若已知水池宽 $ AB = 2a $,芦苇高出水面的部分 $ CD = n(n \lt a) $,则水池的深度 $ OD (OD = b) $ 可以通过公式 $ b = \dfrac{a^{2} - n^{2}}{2n} $ 计算得到. 请说明刘徽解法的正确性.

答案:
13.解:
(1)设芦苇的长为x尺,则OC = OE = x尺,OD = (x - 1)尺,DE = 5尺.在Rt△ODE中,∠ODE = 90°,由勾股定理,得DE² + OD² = OE².5² + (x - 1)² = x²,解得x = 13.
∴OD = 13 - 1 = 12(尺).答:水池的深度OD为12尺.
(2)
∵OD = b,CD = n,AB = 2a,
∴OC = OE = b + n,DE = a.在Rt△ODE中,∠ODE = 90°,由勾股定理,得DE² + OD² = OE².a² + b² = (b + n)²,解得b = (a² - n²)/2n
(1)设芦苇的长为x尺,则OC = OE = x尺,OD = (x - 1)尺,DE = 5尺.在Rt△ODE中,∠ODE = 90°,由勾股定理,得DE² + OD² = OE².5² + (x - 1)² = x²,解得x = 13.
∴OD = 13 - 1 = 12(尺).答:水池的深度OD为12尺.
(2)
∵OD = b,CD = n,AB = 2a,
∴OC = OE = b + n,DE = a.在Rt△ODE中,∠ODE = 90°,由勾股定理,得DE² + OD² = OE².a² + b² = (b + n)²,解得b = (a² - n²)/2n
14. 新考向 数学文化 石家庄外国语校本经典题 《九章算术》是我国古代的数学代表作,书中记载:今有开门去阃(读 kǔn,门槛的意思)一尺,不合二寸,问门广几何? 题目大意:如图 1、图 2(图 2 为图 1 的平面示意图),从点 $ O $ 处推开双门,双门间隙 $ CD $ 的长度为 2 寸,点 $ C $ 和点 $ D $ 到门槛 $ AB $ 的距离都为 1 尺(1 尺 $ = 10 $ 寸),则 $ AB $ 的长是(
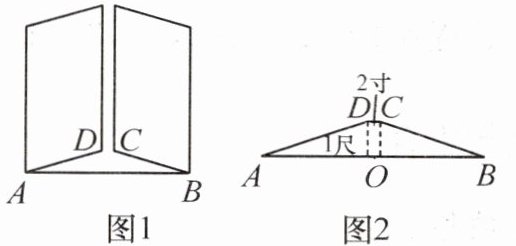
A.104 寸
B.101 寸
C.52 寸
D.50.5 寸
B
)
A.104 寸
B.101 寸
C.52 寸
D.50.5 寸
答案:
14.B
查看更多完整答案,请扫码查看


