第69页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
11. 如图,一次函数 $ y = kx + b $ 的图象经过 $ A $,$ B $ 两点,则关于 $ x $ 的方程 $ kx + b = 0 $ 的解为
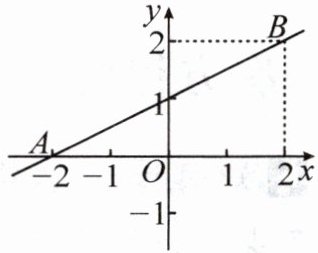
x = -2
.
答案:
11.x = -2
12. 若一次函数 $ y = kx - b $($ k $ 为常数,且 $ k \neq 0 $)的图象经过点 $ (-3, 0) $,则关于 $ x $ 的方程 $ k(x - 7) - b = 0 $ 的解为(
A.$ x = -5 $
B.$ x = -3 $
C.$ x = 4 $
D.$ x = 5 $
C
)A.$ x = -5 $
B.$ x = -3 $
C.$ x = 4 $
D.$ x = 5 $
答案:
12.C
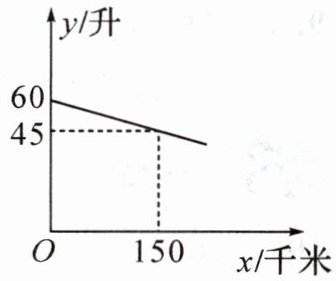
13. 一辆汽车在某次行驶过程中,油箱中的剩余油量 $ y $(升)与行驶路程 $ x $(千米)之间是一次函数关系,其部分图象如图所示.
(1) 求 $ y $ 关于 $ x $ 的函数表达式(不必写出 $ x $ 的取值范围).
(2) 已知当油箱中的剩余油量为 $ 8 $ 升时,该汽车会开始提示加油. 在此次行驶过程中,行驶了 $ 450 $ 千米时,司机发现离前方最近的加油站有 $ 75 $ 千米的路程. 在开往该加油站的途中,当汽车开始提示加油时,离加油站的路程是多少千米?
(1) 求 $ y $ 关于 $ x $ 的函数表达式(不必写出 $ x $ 的取值范围).
(2) 已知当油箱中的剩余油量为 $ 8 $ 升时,该汽车会开始提示加油. 在此次行驶过程中,行驶了 $ 450 $ 千米时,司机发现离前方最近的加油站有 $ 75 $ 千米的路程. 在开往该加油站的途中,当汽车开始提示加油时,离加油站的路程是多少千米?

答案:
13.解:
(1)设y = kx + b,根据题意,得60 = b,① 45 = 150k + b,②将①代入②,得k = -0.1。
∴y关于x的函数表达式为y = -0.1x + 60。
(2)当y = 8时,-0.1x + 60 = 8,解得x = 520。
∴行驶520千米时,油箱中的剩余油量为8升。
∵75 - (520 - 450) = 5(千米),
∴在开往该加油站的途中,当汽车开始提示加油时,离加油站的路程是5千米。
(1)设y = kx + b,根据题意,得60 = b,① 45 = 150k + b,②将①代入②,得k = -0.1。
∴y关于x的函数表达式为y = -0.1x + 60。
(2)当y = 8时,-0.1x + 60 = 8,解得x = 520。
∴行驶520千米时,油箱中的剩余油量为8升。
∵75 - (520 - 450) = 5(千米),
∴在开往该加油站的途中,当汽车开始提示加油时,离加油站的路程是5千米。
14. $ A $ 北师大附属实验校本经典题 图 1 是某公共汽车线路收支差额 $ y $(票价总收入减运营成本)与乘客量 $ x $ 的函数图象. 目前这条线路亏损,为了扭亏,有关部门举行提高票价的听证会.
乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,从而实现扭亏.
公交公司认为:运营成本难以下降,公司已尽力,提高票价才能扭亏.
根据这两种意见,可以把图 1 分别改画成图 2 和图 3.
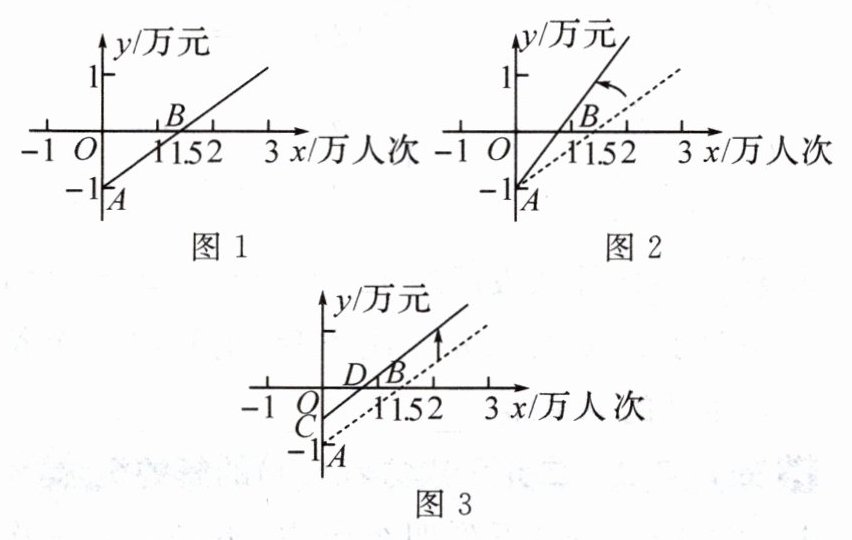
(1) 说明图 1 中点 $ A $ 和点 $ B $ 的实际意义.
(2) 若图 1 改成图 3 后的射线交 $ y $ 轴于点 $ C(0, -0.5) $,交 $ x $ 轴于点 $ D $,射线 $ CD $ 可以看作是由射线 $ AB $ 平移得到,请求出射线 $ CD $ 的表达式,并写出相对应 $ x $ 的取值范围.
(3) 你认为图 2 和图 3 两个图象中,反映乘客意见的是
乘客代表认为:公交公司应节约能源,改善管理,降低运营成本,从而实现扭亏.
公交公司认为:运营成本难以下降,公司已尽力,提高票价才能扭亏.
根据这两种意见,可以把图 1 分别改画成图 2 和图 3.

(1) 说明图 1 中点 $ A $ 和点 $ B $ 的实际意义.
(2) 若图 1 改成图 3 后的射线交 $ y $ 轴于点 $ C(0, -0.5) $,交 $ x $ 轴于点 $ D $,射线 $ CD $ 可以看作是由射线 $ AB $ 平移得到,请求出射线 $ CD $ 的表达式,并写出相对应 $ x $ 的取值范围.
(3) 你认为图 2 和图 3 两个图象中,反映乘客意见的是
图3
,反映公交公司意见的是图2
.
答案:
14.解:
(1)点A表示这条线路的运营成本为1万元;点B表示乘客量达到1.5万人次时,这条线路的收支达到平衡。
(2)设直线AB的表达式为y = kx - 1,把(1.5,0)代入,得1.5k - 1 = 0,解得$k = \frac{2}{3}。$
∴直线AB的表达式为$y = \frac{2}{3}x - 1。$
∵射线CD可以看作是由射线AB平移得到,点C(0,-0.5),
∴射线CD的表达式为$y = \frac{2}{3}x - 0.5(x≥0)。$
(3)图3 图2
(1)点A表示这条线路的运营成本为1万元;点B表示乘客量达到1.5万人次时,这条线路的收支达到平衡。
(2)设直线AB的表达式为y = kx - 1,把(1.5,0)代入,得1.5k - 1 = 0,解得$k = \frac{2}{3}。$
∴直线AB的表达式为$y = \frac{2}{3}x - 1。$
∵射线CD可以看作是由射线AB平移得到,点C(0,-0.5),
∴射线CD的表达式为$y = \frac{2}{3}x - 0.5(x≥0)。$
(3)图3 图2
查看更多完整答案,请扫码查看


