《2025年名校课堂八年级数学上册北师大版内蒙古专版》

6. (教材P120例1变式)我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题：“甲乙隔沟牧放，二人暗里参详，甲云得乙九只羊，多乙一倍之上，乙说得甲九只，两家之数相当，二人闲坐恼心肠，画地算了半晌.”其大意为：甲、乙两人一起放牧，两人心里暗中数羊.如果乙给甲9只羊，那么甲的羊数为乙的2倍；如果甲给乙9只羊，那么两人的羊数相同.请问甲、乙各有多少只羊？设甲有$x$只羊，乙有$y$只羊，根据题意列方程组正确的为(D)

A.$\begin{cases}2x + 9 = y - 9,\\x - 9 = 2y + 9\end{cases}$
B.$\begin{cases}x + 9 = 2y - 9,\\2x - 9 = y + 9\end{cases}$
C.$\begin{cases}2(x + 9) = y - 9,\\x - 9 = y + 9\end{cases}$
D.$\begin{cases}x + 9 = 2(y - 9),\\x - 9 = y + 9\end{cases}$

答案： 6.D

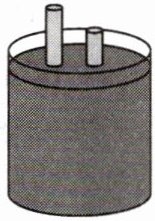
7. 如图，两根铁棒直立于桶底水平的水桶中，向桶中加水，其中一根铁棒露出水面的长度是它的$\frac{1}{3}$，另一根铁棒露出水面的长度是它的$\frac{1}{5}$，两根铁棒的长度之和为55 cm，则较长铁棒的长度为30 cm，较短铁棒的长度为25 cm.

答案： 7.30 25

8. 《九章算术》是我国古代经典的数学著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等.交易其一，金轻十二两.问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚(每枚黄金质量相同)，乙袋中装有白银11枚(每枚白银质量相同)，两袋质量相等，两袋互相交换1枚后，甲袋比乙袋轻了12两(袋子质量相同).问黄金、白银每枚各重多少两？

答案： 解：设每枚黄金重$x$两，每枚白银重$y$两。
根据“甲袋中装有黄金$9$枚，乙袋中装有白银$11$枚，两袋质量相等”，可列方程$9x = 11y$ ①；
根据“两袋互相交换$1$枚后，甲袋比乙袋轻了$12$两”，此时甲袋有$(9 - 1)$枚黄金和$1$枚白银，乙袋有$(11 - 1)$枚白银和$1$枚黄金，可列方程$(10y + x)-(8x + y)=12$ ②。
由②式得：
$\begin{aligned}10y + x - 8x - y&=12\\9y - 7x&=12\\9y&=7x + 12\\y&=\frac{7x + 12}{9}\end{aligned}$
把$y=\frac{7x + 12}{9}$代入①式得：
$\begin{aligned}9x&=11×\frac{7x + 12}{9}\\81x&=11×(7x + 12)\\81x&=77x + 132\\81x - 77x&=132\\4x&=132\\x&=33\end{aligned}$
把$x = 33$代入$y=\frac{7x + 12}{9}$得：
$y=\frac{7×33 + 12}{9}=\frac{231 + 12}{9}=\frac{243}{9}=27$
所以黄金每枚重$33$两，白银每枚重$27$两。

9. 随着“低碳生活，绿色出行”理念的普及，新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售，据了解，2辆A型汽车、3辆B型汽车的进价共计80万元，3辆A型汽车、2辆B型汽车的进价共计95万元.
(1) 求A，B两种型号的汽车每辆进价分别为多少万元.
(2) 若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买)，请帮助该公司设计购买方案.
(3) 若该汽车销售公司销售1辆A型汽车可获利8000元，销售1辆B型汽车可获利5000元，在(2)的购买方案中，假如这些新能源汽车全部售出，哪种方案获利最大？最大利润是多少元？

答案： 9.解：
(1)设A型汽车每辆的进价为x万元，B型汽车每辆的进价为y万元.依题意，得$\begin{cases}2x + 3y = 80,\\3x + 2y = 95,\end{cases}$解得$\begin{cases}x = 25,\\y = 10.\end{cases}$答：A型汽车每辆的进价为25万元，B型汽车每辆的进价为10万元.
(2)设购进A型汽车m辆，购进B型汽车n辆.依题意，得25m + 10n = 200，解得m = 8 - $\frac{2}{5}n$.
∵m，n均为正整数，
∴$\begin{cases}m_1 = 6,\\n_1 = 5,\end{cases}$$\begin{cases}m_2 = 4,\\n_2 = 10,\end{cases}$$\begin{cases}m_3 = 2,\\n_3 = 15.\end{cases}$
∴共有3种购买方案，方案1：购进A型汽车6辆，B型汽车5辆；方案2：购进A型汽车4辆，B型汽车10辆；方案3：购进A型汽车2辆，B型汽车15辆.
(3)方案1获得利润：8000×6 + 5000×5 = 73000(元)；方案2获得利润：8000×4 + 5000×10 = 82000(元)；方案3获得利润：8000×2 + 5000×15 = 91000(元).
∵73000 ＜ 82000 ＜ 91000，
∴购进A型汽车2辆，B型汽车15辆获利最大，最大利润是91000元.