第26页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 化简:
(1)$\sqrt{25×49}=$
(2)$\sqrt{16×3}=$
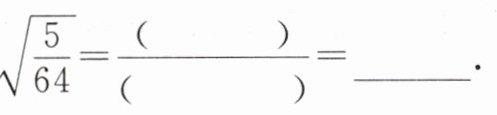
(3)
(1)$\sqrt{25×49}=$
$\sqrt{25}$
×$\sqrt{49}$
=5
×7
=35
.(2)$\sqrt{16×3}=$
$\sqrt{16}$
×$\sqrt{3}$
=4
×$\sqrt{3}$
=$4\sqrt{3}$
.(3)

答案:
1.
(1)$\sqrt{25}$ $\sqrt{49}$ 5 7 35
(2)$\sqrt{16}$ $\sqrt{3}$ 4 $\sqrt{3}$ 4$\sqrt{3}$
(3)$\sqrt{5}$ $\sqrt{64}$ $\frac{\sqrt{5}}{8}$
(1)$\sqrt{25}$ $\sqrt{49}$ 5 7 35
(2)$\sqrt{16}$ $\sqrt{3}$ 4 $\sqrt{3}$ 4$\sqrt{3}$
(3)$\sqrt{5}$ $\sqrt{64}$ $\frac{\sqrt{5}}{8}$
2. 若$\sqrt{\frac{x+1}{2-x}}=\frac{\sqrt{x+1}}{\sqrt{2-x}}$成立,则$x$的值可以是(
A.$-2$
B.$0$
C.$2$
D.$3$
B
)A.$-2$
B.$0$
C.$2$
D.$3$
答案:
2.B
3. 下列式子成立的是(
A.$\sqrt{(-4)^2}=-4$
B.$\sqrt{4×3}=\sqrt{4}×\sqrt{3}$
C.$\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{4}$
D.$\sqrt{(-4)×(-3)}=\sqrt{-4}×\sqrt{-3}$
B
)A.$\sqrt{(-4)^2}=-4$
B.$\sqrt{4×3}=\sqrt{4}×\sqrt{3}$
C.$\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{4}$
D.$\sqrt{(-4)×(-3)}=\sqrt{-4}×\sqrt{-3}$
答案:
3.B
4. 计算:
(1)$\sqrt{4×225}$.
(2)$\sqrt{81×7}$.
(3)$\sqrt{\frac{4×2}{25}}$.
(1)$\sqrt{4×225}$.
(2)$\sqrt{81×7}$.
(3)$\sqrt{\frac{4×2}{25}}$.
答案:
4.解:
(1)原式=$\sqrt{4 × 225}=2 × 15 = 30$.
(2)原式=$\sqrt{81 × 7}=9\sqrt{7}$.
(3)原式=$\frac{\sqrt{4 × 2}}{\sqrt{25}}=\frac{2\sqrt{2}}{5}$.
(1)原式=$\sqrt{4 × 225}=2 × 15 = 30$.
(2)原式=$\sqrt{81 × 7}=9\sqrt{7}$.
(3)原式=$\frac{\sqrt{4 × 2}}{\sqrt{25}}=\frac{2\sqrt{2}}{5}$.
5. 下列二次根式中,属于最简二次根式的是(
A.$\sqrt{4}$
B.$\sqrt{5}$
C.$\sqrt{8}$
D.$\sqrt{\frac{1}{2}}$
B
)A.$\sqrt{4}$
B.$\sqrt{5}$
C.$\sqrt{8}$
D.$\sqrt{\frac{1}{2}}$
答案:
5.B
6. (2024·包头)计算$\sqrt{9^2-6^2}$的结果是(
A.$3$
B.$\sqrt{6}$
C.$3\sqrt{5}$
D.$\pm3\sqrt{5}$
C
)A.$3$
B.$\sqrt{6}$
C.$3\sqrt{5}$
D.$\pm3\sqrt{5}$
答案:
6.C
7. 化简:
(1)$\sqrt{12}$.
(2)$\sqrt{75}$.
(3)$\sqrt{2.5}$.
(4)$\frac{\sqrt{27}}{3}$.
(5)$\sqrt{\frac{8}{9}}$.
(6)$\sqrt{\frac{8}{5}}$.
(1)$\sqrt{12}$.
(2)$\sqrt{75}$.
(3)$\sqrt{2.5}$.
(4)$\frac{\sqrt{27}}{3}$.
(5)$\sqrt{\frac{8}{9}}$.
(6)$\sqrt{\frac{8}{5}}$.
答案:
7.解:
(1)原式=$2\sqrt{3}$.
(2)原式=$5\sqrt{3}$.
(3)原式=$\sqrt{\frac{5}{2}}=\frac{\sqrt{10}}{2}$
(4)原式=$\frac{3\sqrt{3}}{3}=\sqrt{3}$.
(5)原式=$\frac{\sqrt{8}}{3}=\frac{2\sqrt{2}}{3}$.
(6)原式=$\frac{\sqrt{40}}{5}=\frac{2\sqrt{10}}{5}$.
(1)原式=$2\sqrt{3}$.
(2)原式=$5\sqrt{3}$.
(3)原式=$\sqrt{\frac{5}{2}}=\frac{\sqrt{10}}{2}$
(4)原式=$\frac{3\sqrt{3}}{3}=\sqrt{3}$.
(5)原式=$\frac{\sqrt{8}}{3}=\frac{2\sqrt{2}}{3}$.
(6)原式=$\frac{\sqrt{40}}{5}=\frac{2\sqrt{10}}{5}$.
8. 下列二次根式中,不能与$\sqrt{5}$合并的是(
A.$2\sqrt{5}$
B.$\sqrt{15}$
C.$\sqrt{20}$
D.$\frac{1}{\sqrt{5}}$
B
)A.$2\sqrt{5}$
B.$\sqrt{15}$
C.$\sqrt{20}$
D.$\frac{1}{\sqrt{5}}$
答案:
8.B
9. 计算:
(1)$\sqrt{8}+\sqrt{2}=$
(2)(2024·长春)$\sqrt{12}-\sqrt{3}=$
(3)(2024·威海)$\sqrt{12}-\sqrt{8}×\sqrt{6}=$
(1)$\sqrt{8}+\sqrt{2}=$
$3\sqrt{2}$
.(2)(2024·长春)$\sqrt{12}-\sqrt{3}=$
$\sqrt{3}$
.(3)(2024·威海)$\sqrt{12}-\sqrt{8}×\sqrt{6}=$
$-2\sqrt{3}$
.
答案:
9.
(1)$3\sqrt{2}$
(2)$\sqrt{3}$
(3)$-2\sqrt{3}$
(1)$3\sqrt{2}$
(2)$\sqrt{3}$
(3)$-2\sqrt{3}$
10. 计算:
(1)$\sqrt{75}+\sqrt{48}$.
(2)$\sqrt{8}-\sqrt{\frac{9}{2}}$.
(3)$(\sqrt{24}-\sqrt{\frac{8}{3}})×\sqrt{3}$.
(1)$\sqrt{75}+\sqrt{48}$.
(2)$\sqrt{8}-\sqrt{\frac{9}{2}}$.
(3)$(\sqrt{24}-\sqrt{\frac{8}{3}})×\sqrt{3}$.
答案:
10.解:
(1)原式=$5\sqrt{3}+4\sqrt{3}=9\sqrt{3}$.
(2)原式=$2\sqrt{2}-\frac{3\sqrt{2}}{2}=\frac{\sqrt{2}}{2}$.
(3)原式=$\sqrt{24 × 3}-\sqrt{\frac{8}{3} × 3}=\sqrt{72}-\sqrt{8}=6\sqrt{2}-2\sqrt{2}=4\sqrt{2}$.
(1)原式=$5\sqrt{3}+4\sqrt{3}=9\sqrt{3}$.
(2)原式=$2\sqrt{2}-\frac{3\sqrt{2}}{2}=\frac{\sqrt{2}}{2}$.
(3)原式=$\sqrt{24 × 3}-\sqrt{\frac{8}{3} × 3}=\sqrt{72}-\sqrt{8}=6\sqrt{2}-2\sqrt{2}=4\sqrt{2}$.
查看更多完整答案,请扫码查看


