《2025年实验班提优训练七年级数学上册人教版》

【例1】(第九届“枫叶新希望杯”全国数学大赛)已知$a_{1},a_{2},a_{3},...,a_{2013}$都是正有理数,$M= (a_{1}+a_{2}+a_{3}+... +a_{2012})(a_{2}+a_{3}+a_{4}+... +a_{2013})$,$N= (a_{1}+a_{2}+a_{3}+... +a_{2013})(a_{2}+a_{3}+a_{4}+... +a_{2012})$,则$M$,$N$的大小关系为(A)。
A.$M＞N$
B.$M＜N$
C.$M= N$
D.无法确定
解析：设$a_{1}+a_{2}+a_{3}+... +a_{2012}= x$,$a_{2}+a_{3}+a_{4}+... +a_{2012}= y$,
则$M= x(y+a_{2013})$,$N= (x+a_{2013})y$,
$\therefore M-N= x(y+a_{2013})-(x+a_{2013})y= (x-y)a_{2013}= a_{1}a_{2013}＞0$,
$\therefore M＞N$。
答案：A

答案： 解：设$a_{1}+a_{2}+a_{3}+\dots +a_{2012}=x$，$a_{2}+a_{3}+\dots +a_{2012}=y$，则$M = x(y + a_{2013})$，$N=(x + a_{2013})y$。
$M - N=x(y + a_{2013})-(x + a_{2013})y$
$=xy + xa_{2013}-xy - ya_{2013}$
$=(x - y)a_{2013}$
因为$x - y=(a_{1}+a_{2}+\dots +a_{2012})-(a_{2}+\dots +a_{2012})=a_{1}$，且$a_{1},a_{2013}$为正有理数，所以$(x - y)a_{2013}=a_{1}a_{2013}＞0$，即$M - N＞0$，故$M＞N$。
答案：A

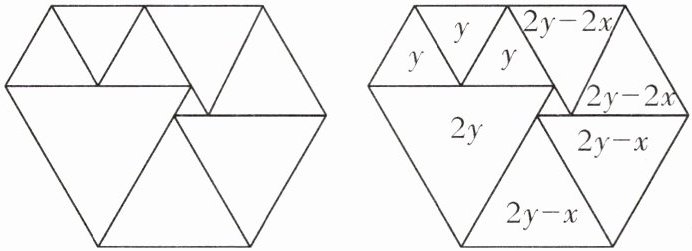
【例2】(第九届“枫叶新希望杯”全国数学大赛)如图,六边形是由9个等边三角形拼成的,若中间的小等边三角形的周长为$a$,那么六边形的周长为(B)。

A.$9a$
B.$10a$

C.$11a$
D.$12a$
解析：设中间的三角形边长为$x$,左上角的三角形边长为$y$,
如图所示,可知$x+y= 2y-2x$,则$y= 3x$,
六边形的周长为$2y+2y+(2y-x)×2+(2y-2x)×2= 12y-6x= 30x= 10a$。
答案：B

答案： 【解析】：本题可通过设未知数，根据等边三角形的性质找出各边之间的关系，进而求出六边形的周长。
设中间小等边三角形的边长为$x$，因为中间小等边三角形周长为$a$，根据等边三角形周长等于边长的$3$倍，可得$3x = a$，即$x=\frac{a}{3}$。
设左上角等边三角形的边长为$y$，观察图形可知，与$y$相关的边存在等量关系：$x + y = 2y - 2x$，移项可得$y = 3x$。
接下来求六边形的周长，六边形的周长由各等边三角形的边组成，将六边形各边用$x$和$y$表示出来并求和：
六边形的周长为$2y + 2y + (2y - x)×2 + (2y - 2x)×2$，
将$y = 3x$代入上式可得：
$2×3x + 2×3x + (2×3x - x)×2 + (2×3x - 2x)×2$
$= 6x + 6x + (6x - x)×2 + (6x - 2x)×2$
$= 12x + 5x×2 + 4x×2$
$= 12x + 10x + 8x$
$= 30x$
再把$x=\frac{a}{3}$代入$30x$，可得$30×\frac{a}{3}=10a$。
【答案】：B

1. (第13届“枫叶新希望杯”全国数学大赛七年级试题)现有一列数$m_{1},m_{2},m_{3},...,m_{2010}$,其中,$m_{2}= -1$,$m_{7}= -7$,$m_{99}= 9$,且$m_{n}+m_{n+1}+m_{n+2}= 1$($n$为正整数),则$m_{1}+m_{2}+... +m_{2010}=$(C)。
A.668
B.669
C.670
D.671

答案： 1.C ［解析］
∵m₂=-1，m₇=-7，m₅₉=9，且mₙ+mₙ₊₁+mₙ₊₂=1，
∴依次每三项的和为1，
∴m₁=m₇=-7，m₃=m₅₉=9，
∴该数列从第1个数起，以-7，-1，9这3个数循环出现.
∵2010÷3=670.
∴m₁+m₂+…+m₂₀₁₀=1×670=670.故选C.

2. (第13届“枫叶新希望杯”全国数学大赛初中试卷)将1,2,3,…,200这200个自然数,任意分成100组,每组两个数,记第$k组中的两个数记为a_{k}$,$b_{k}$,若$S_{k}= \frac {a_{k}+b_{k}+|a_{k}-b_{k}|}{2}$,则$S_{1}+S_{2}+S_{3}+... +S_{100}$的最小值为10100。

答案： 2.10100 ［解析］当aₖ＞bₖ时，Sₖ=$\frac{a_k+b_k+|a_k-b_k|}{2}$=$\frac{a_k+b_k+a_k-b_k}{2}$=aₖ；当aₖ＜bₖ时，Sₖ=$\frac{a_k+b_k+|a_k-b_k|}{2}$=$\frac{a_k+b_k-a_k+b_k}{2}$=bₖ，
∴将每组中的两个数aₖ和bₖ，分别代入代数式后计算的结果等于两个数中较大的数.
∴S₁+S₂+S₃+…+S₁₀₀的最小值为2+4+6+8+…+198+200=$\frac{(2+200)×100}{2}$=10100.

3. (第九届优利信杯竞赛)[阅读]
$1×2= \frac {1}{3}(1×2×3-0×1×2)$；$2×3= \frac {1}{3}(2×3×4-1×2×3)$；$3×4= \frac {1}{3}(3×4×5-2×3×4)$；
将这三个等式的两边相加,则得到$1×2+2×3+3×4= \frac {1}{3}×3×4×5= 20$。
[归纳](1)根据上述规律,猜想下列等式的结果：$1×2+2×3+... +n(n+1)= $$\frac{1}{3}$n(n+1)(n+2)；
[应用](2)利用(1)中得到的结论计算：$2×4+4×6+... +100×102$；
2×4+4×6+…+100×102=4×(1×2+2×3+…+50×51)=4×$\frac{1}{3}$×50×51×52=176800.
[迁移](3)请你类比材料中的方法计算：$1×2×3+2×3×4+... +n(n+1)(n+2)$。
1×2×3+2×3×4+…+n(n+1)(n+2)=$\frac{1}{4}$×(1×2×3×4-0×1×2×3)+$\frac{1}{4}$×(2×3×4×5-1×2×3×4)+…+$\frac{1}{4}$×[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]=$\frac{1}{4}$×[1×2×3×4-0×1×2×3+2×3×4×5-1×2×3×4+…+n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]=$\frac{1}{4}$n(n+1)(n+2)(n+3).

答案： 3.
(1)$\frac{1}{3}$n(n+1)(n+2) ［解析］1×2+2×3+3×4=$\frac{1}{3}$×3×4×5，1×2+2×3+3×4+4×5=$\frac{1}{3}$×4×5×6，…，
∴1×2+2×3+…+n(n+1)=$\frac{1}{3}$n(n+1)(n+2).
(2)2×4+4×6+…+100×102=4×(1×2+2×3+…+50×51)=4×$\frac{1}{3}$×50×51×52=176800.
(3)1×2×3+2×3×4+…+n(n+1)(n+2)=$\frac{1}{4}$×(1×2×3×4-0×1×2×3)+$\frac{1}{4}$×(2×3×4×5-1×2×3×4)+…+$\frac{1}{4}$×[n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]=$\frac{1}{4}$×[1×2×3×4-0×1×2×3+2×3×4×5-1×2×3×4+…+n(n+1)(n+2)(n+3)-(n-1)n(n+1)(n+2)]=$\frac{1}{4}$n(n+1)(n+2)(n+3).