《2025年实验班提优训练七年级数学上册人教版》

9. 黑板上写着7个数,分别为-8,a,1,13,b,0,-6,它们的和为-10,若每次从中任意擦除两个数,同时写上一个新数(新数为所擦除的两个数的和加上1),这样操作若干次,直至黑板上只剩下一个数,则所剩的这个数是____-4.

答案： -4 解析 根据题意,得-8+a+1+13+b+0-6=-10,
∴a+b=-10.先擦掉a,b,新加的数为-9,可得-8,-9,1,13,0,-6;擦掉前两个数,新加一个数,依次可得-16,1,13,0,-6;-14,13,0,-6;0,0,-6;1,-6;-4.故最后所剩的数是-4.

10. (2025·云南昆明期中)计算:
(1)$(\frac {1}{3}+\frac {1}{4}-\frac {1}{6})×(-24)-(-2)×5;$
(2)$-3^{2}+(-2+5)^{2}-|-\frac {1}{4}|×(-3)^{2}.$

答案：
(1)原式$=\frac{1}{3}×(-24)+\frac{1}{4}×(-24)-\frac{1}{6}×(-24)+10=-8-6+4+10=0.(2)$原式$=-9+9-\frac{1}{4}×9=-\frac{9}{4}.$思路引导 本题考查了有理数的加减运算、有理数的混合运算、有理数的乘法运算律等知识点,熟练掌握有理数混合运算法则是解题的关键.

11. (2025·吉林长春期中)如果对于任何有理数a,b定义运算“△”如下：$a△b= \frac {1}{a}÷(-\frac {b}{2})$,如$2△3= \frac {1}{2}÷(-\frac {3}{2})= -\frac {1}{3}$.
(1)求$-1△2$的值;
(2)求$(-2△7)△4$的值.

答案：
(1)
∵$a△b=\frac{1}{a}÷(-\frac{b}{2}),$
∴$-1△2=-1÷(-\frac{2}{2})=-1÷(-1)=1.(2)$
∵$a△b=\frac{1}{a}÷(-\frac{b}{2}),$
∴$-2△7=-\frac{1}{2}÷(-\frac{7}{2})=-\frac{1}{2}×(-\frac{2}{7})=\frac{1}{7},$
∴$(-2△7)△4=\frac{1}{7}△4=7÷(-\frac{4}{2})=7÷(-2)=-\frac{7}{2}.$思路引导 本题考查新定义运算,有理数的混合运算,掌握运算顺序与运算法则是解决问题的关键.

12. 如图,小明有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
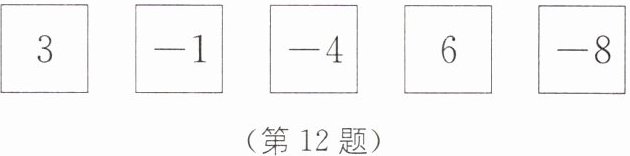
(1)若从中抽出2张卡片,且这2个数字的差最小,应如何抽取? 最小值是多少?
(2)若从中抽出2张卡片,且这2个数字的积最大,应如何抽取? 最大值是多少?
(3)若从中抽出4张卡片,运用加、减、乘、除、乘方、括号等运算符号,使得结果为24,请写出运算式.(只需写出1种)

答案：
(1)抽取的2张卡片是-8,6,它们的差最小,最小值是-8-6=-14.
(2)抽取的2张卡片是-4,-8,它们的积最大,最大值是(-4)×(-8)=32.
(3)抽取的4张卡片是3,-4,6,-8,算式为(-8+6)×3×(-4)=24(答案不唯一).

13. 已知某粮库已存有粮食100吨,某周内粮库进出粮食的记录如下(运进为正,运出为负).
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 进出粮食/吨 | +35 | -20 | -30 | +25 | -24 | +50 | -26 |
(1)通过计算,说明这周内哪天粮库剩余的粮食最多,是多少?
(2)若运进的粮食为购进的,购买的价格为每吨2000元,运出的粮食为卖出的,卖出的价格为每吨2300元,则这一周的利润为多少元?
(3)若每周平均进出的粮食数量大致相同(误差忽略不计),则再过几周粮库存的粮食可达到200吨?

答案：
(1)星期一:100+35=135(吨),星期二:135-20=115(吨),星期三:115-30=85(吨),星期四:85+25=110(吨),星期五:110-24=86(吨),星期六:86+50=136(吨),星期日:136-26=110(吨),故星期六剩余的粮食最多,是136吨.
(2)2300×(20+30+24+26)-2000×(35+25+50)=10000(元),故这一周的利润为10000元.
(3)(200-100)÷(+35-20-30+25-24+50-26)-1=9(周).故再过9周粮库存的粮食可达到200吨.
思路引导 本题考查了正负数的意义,有理数加减、混合运算的实际应用,根据题意正确列出算式是解题的关键.