《2025年实验班提优训练七年级数学上册人教版》

7. 传统文化《九章算术》(2025·平凉一模)《九章算术》中记载了这样一个数学问题:今有甲发长安,五日至齐;乙发齐,七日至长安.今乙发已先二日,甲仍发长安.问几何日相逢? 译文:甲从长安出发,5日到齐国;乙从齐国出发,7日到长安.现乙先出发2日,甲才从长安出发.问多久后甲、乙相逢? 设乙出发x日,甲、乙相逢,则可列方程为(D).
A.$\frac {x+2}{7}+\frac {x}{5}= 1$
B.$\frac {x-2}{7}+\frac {x}{5}= 1$
C.$\frac {x}{7}+\frac {x+2}{5}= 1$
D.$\frac {x}{7}+\frac {x-2}{5}= 1$

答案： D [解析]设乙出发x日，甲、乙相逢. 根据题意，得$\frac{x}{7}+\frac{x-2}{5}=1$. 故选 D.思路引导 本题考查一元一次方程的应用，理解题意，找准等量关系是解答的关键. 设两地距离为1，先求得甲、乙的速度分别为$\frac{1}{5}$，$\frac{1}{7}$，再根据相遇时，两人所走路程和为1列方程求解即可.

8. (2025·浙江宁波镇海区期中)某同学解关于x的方程,$\frac {3x-1}{3}= 1-\frac {4x+a}{6}$,在去分母时,漏乘方程右边的常数项,求得错误的解为$x= 2$,则$a=$-17,该方程正确的解为$x=$2.5.

答案： -17 2.5 [解析]
∵方程$\frac{3x-1}{3}=1-\frac{4x+a}{6}$，在去分母时，漏乘方程右边的常数项，
∴去分母，得$2(3x-1)=1-(4x+a)$. 将$x=2$代入，得$10=1-(8+a)$，解得$a=-17$，
∴原方程为$\frac{3x-1}{3}=1-\frac{4x-17}{6}$，解得$x=2.5$.思路引导 本题考查解一元一次方程，正确掌握解法是解题的关键，先根据题意去分母，将$x=2$代入求出a的值，再将a代回原方程求出方程的解.

9. 一列方程如下排列:$\frac {x}{4}+\frac {x-1}{2}= 1的解是x= 2$,
$\frac {x}{6}+\frac {x-2}{2}= 1的解是x= 3$,
$\frac {x}{8}+\frac {x-3}{2}= 1的解是x= 4$,
…,
根据观察得到的规律,写出解是$x= 2025$的方程:$\frac{x}{4050}+\frac{x-2024}{2}=1$.

答案： $\frac{x}{4050}+\frac{x-2024}{2}=1$ [解析]
∵一列方程如下排列：$\frac{x}{4}+\frac{x-1}{2}=1$的解是$x=2$；$\frac{x}{6}+\frac{x-2}{2}=1$的解是$x=3$；$\frac{x}{8}+\frac{x-3}{2}=1$的解是$x=4$，
∴一列方程如下排列：$\frac{x}{2×2}+\frac{x-(2-1)}{2}=1$的解是$x=2$；$\frac{x}{2×3}+\frac{x-(3-1)}{2}=1$的解是$x=3$；$\frac{x}{2×4}+\frac{x-(4-1)}{2}=1$的解是$x=4$；…，由此可得解为$x=2025$的方程为$\frac{x}{2×2025}+\frac{x-(2025-1)}{2}=1$，即$\frac{x}{4050}+\frac{x-2024}{2}=1$.思路引导 本题考查了一元一次方程的解，能根据题意得出规律是解此题的关键. 先根据已知方程得出规律，再根据得出的规律得出答案即可.

10. 教材P128例7·变式 小红在解方程$\frac {7x}{3}= \frac {4x-1}{6}+1$时,第一步出现了错误: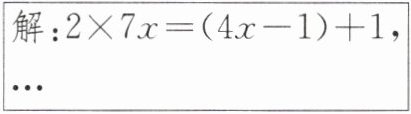
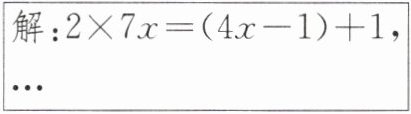
(1)请在相应的方框内用横线划出小红的错误处;
(2)写出你的解答过程.

答案：
(1)如下：解：$2×7x=(4x-1)+1$，…
(2)去分母，得$2×7x=(4x-1)+6$，去括号，得$14x=4x-1+6$，移项，得$14x-4x=-1+6$，合并同类项，得$10x=5$，系数化为1，得$x=\frac{1}{2}$.

11. 小玲在解方程$\frac {2x-1}{3}= \frac {x+a}{2}-1$去分母时,忘记将方程右边的“-1”乘6,因而求得了方程的解为$x= 2$.请根据上述信息:
(1)求a的值;
(2)求方程正确的解.

答案：
(1)$\frac{2x-1}{3}=\frac{x+a}{2}-1$，去分母，得$2(2x-1)=3(x+a)-6$，把$x=2$代入方程$2(2x-1)=3(x+a)-1$，得$2×(4-1)=3(2+a)-1$，解得$a=\frac{1}{3}$.
(2)原方程为$\frac{2x-1}{3}=\frac{x+\frac{1}{3}}{2}-1$，去分母，得$2(2x-1)=3(x+\frac{1}{3})-6$，去括号，得$4x-2=3x+1-6$，移项，得$4x-3x=-6+1+2$，解得$x=-3$.关键提醒 本题考查了一元一次方程的解、解一元一次方程的应用，解此题的关键是能得出关于a的方程.