《2025年实验班提优训练七年级数学上册人教版》

6. 传统文化《九章算术》(2025·重庆期末)数学老师根据我国古代数学名著《九章算术》方程篇改编了一道题:贩粟归梓,空车日行百里,满载日行六十,十一日二返,外地几何?大意为:去外地采购谷物回乡,空车日行100里,装满后日行60里,11天往返乡里两次,求到外地有多少里?设到外地有x里,则可列方程为(A).
A.$\frac {2x}{100}+\frac {2x}{60}= 11$
B.$\frac {x}{100}+\frac {x}{60}= 11$
C.$\frac {4x}{100+60}= 11$
D.$\frac {2x}{100}+\frac {2x}{60}= \frac {11}{2}$

答案： A [解析]设到外地有$x$里.由题意,得$\frac{2x}{100}+\frac{2x}{60}=11$.故选 A.
归纳总结 本题考查了一元一次方程的应用,设到外地有$x$里,由题意列出方程$\frac{2x}{100}+\frac{2x}{60}=11$即可,读懂题意,找出等量关系,列出方程是解题的关键.

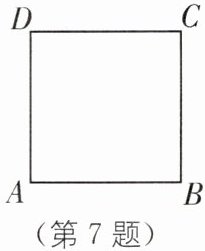
7. (2025·新疆乌鲁木齐一中期末)如图,正方形ABCD的边长是2个单位长度,一只乌龟从点A出发以2个单位长度/秒的速度顺时针绕正方形运动,另有一只兔子也从点A出发以6个单位长度/秒的速度逆时针绕正方形运动,则第2025次相遇在(B).

A.点A
B.点D
C.点C
D.点B

答案： B [解析]设$x$秒时,它们第2025次相遇.根据题意,得$2x+6x=2× 4× 2025$,解得$x=2025$,$\therefore 2x=4050$.
$\because 4050÷ (2× 4)=506\cdots \cdots 2$,
$\therefore$它们第2025次相遇在点 D.故选 B.

8. (2025·河南郑州中牟期末)已知A,B两地相距200千米,甲车以80千米/时的速度从A地出发,乙车以60千米/时的速度从B地出发,乙车在前,甲车在后.如果两车同时出发,同向而行,那么出发后9或11小时,两车相距20千米.

答案： 9或11 [解析]设出发后$x$小时,两车相距20千米,分两种情况:
①追上相距20千米:
$(80-60)x=200-20$,解得$x=9$;
②追上后超过20千米:
$(80-60)x=200+20$,解得$x=11$.

9. 一题多解思想下面是学习一元一次方程的应用时,老师出示的问题和两名同学所列的方程.
货车和客车从A,B两地同时相向而行,货车的平均速度为96km/h,客车的平均速度为84km/h,两车在离中点18km处相遇,求A,B两地相距多少千米?
乐乐同学:$96x-18= 84x+18$.
丽丽同学:$\frac {y+18}{96}= \frac {y-18}{84}$.
请根据以上信息,解答下列问题:
(1)乐乐同学所列方程中x表示的实际意义是两车相遇时间;丽丽同学所列方程中y表示的实际意义是A,B两地到中点的路程;
(2)请你选择其中一名同学的解法完成上面的问题;
乐乐同学的解法:
设两车$x$小时相遇,则$96x-18=84x+18$,解得$x=3$,
$\therefore$A,B两地的路程为$96× 3+84× 3=540$(千米);
(3)完成上述问题后,结合你平时的学习经验,就如何利用一元一次方程解决实际问题给同学们提一条建议.
尝试一题多种解法.

答案：
(1)两车相遇时间 A,B两地到中点的路程
(2)乐乐同学的解法:
设两车$x$小时相遇,则$96x-18=84x+18$,解得$x=3$,
$\therefore$A,B两地的路程为$96× 3+84× 3=540$(千米);
丽丽同学的解法:
设A,B两地到中点的路程为$y$千米,则$\frac{y+18}{96}=\frac{y-18}{84}$,解得$y=270$,
$\therefore$A,B两地间的路程为$270× 2=540$(千米).
(3)尝试一题多种解法.
思路引导 本题主要考查了一元一次方程的应用——行程问题,熟练掌握路程与时间的关系,掌握一题多解的思维,是解决问题的关键.

10. A,B两地相距360km,一辆小轿车和一辆货车分别沿同一条路线从A地出发驶往B地.已知货车的速度为60km/h,小轿车的速度为90km/h,货车先出发1h后小轿车再出发,小轿车到达B地后在原地等货车.
(1)求小轿车出发多长时间追上货车;
(2)求小轿车出发多长时间后,两车相距50km.

答案：
(1)设小轿车出发$x$h追上货车.
根据题意,得$60+60x=90x$,解得$x=2$.
故小轿车出发2h追上货车.
(2)设小轿车出发后$t$h,两车相距50km.
①小轿车出发后在追上货车之前,两车相距50km,则$60+60t=90t+50$,解得$t=\frac{1}{3}$;
②小轿车超过货车且未到B地,两车相距50km,则$60+60t+50=90t$,解得$t=\frac{11}{3}$;
③小轿车到达B地后在原地等货车,两车相距50km,则$60+60t+50=360$,解得$t=\frac{25}{6}$.
故小轿车出发$\frac{1}{3}$h或$\frac{11}{3}$h或$\frac{25}{6}$h后,两车相距50km.