第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1. (2025·浙江温州期中)数轴上点A向右移动3个单位长度得到点B,若点B表示的数为2,则点A表示的数为(
A.-1
B.1
C.-5
D.5
A
).A.-1
B.1
C.-5
D.5
答案:
A [解析]
∵点A向右移动3个单位长度得到点B,点B 表示的数为2,
∴点B向左移动3个单位长度得到点A,
∴点A表示的数为−1.故选A
∵点A向右移动3个单位长度得到点B,点B 表示的数为2,
∴点B向左移动3个单位长度得到点A,
∴点A表示的数为−1.故选A
2. (2025·浙江绍兴期中)M点在数轴上表示-3,N点离M点的距离是4,那么N点表示的数为( ).
A.1
B.-7
C.1或-7
D.-1或7
A.1
B.-7
C.1或-7
D.-1或7
答案:
C [解析]如图所示:
∵M点在数轴上表示−3,N点离M点的距离是4,N点表示的数为−3+4=1或−3−4=−7.已知距离反求原数时一定要注意分类讨论故选C.
C [解析]如图所示:

∵M点在数轴上表示−3,N点离M点的距离是4,N点表示的数为−3+4=1或−3−4=−7.已知距离反求原数时一定要注意分类讨论故选C.
3. 分类讨论思想(2025·广东深圳期中)一只蚂蚁沿数轴从点A向一个方向移动了2个单位长度到达点B,若点B表示的数是-3,则点A所表示的数是(
A.-5或-1
B.-5或1
C.-5
D.1
A
).A.-5或-1
B.-5或1
C.-5
D.1
答案:
A [解析]
∵点B表示的数是−3,
∴当蚂蚁沿数轴从点A向左移动了2个单位长度时,点A 所表示的数是−1,当蚂蚁沿数轴从点A向右移动了2个单位长度时,点A 所表示的数是−5,
∴点A所表示的数是−5或−1.故选A 易错警示 本题考查了数轴与有理数,根据点B表示的数,分向左和向右两种情况讨论即可求出答案,明确数轴的特点,分情况讨论是解题的关键
∵点B表示的数是−3,
∴当蚂蚁沿数轴从点A向左移动了2个单位长度时,点A 所表示的数是−1,当蚂蚁沿数轴从点A向右移动了2个单位长度时,点A 所表示的数是−5,
∴点A所表示的数是−5或−1.故选A 易错警示 本题考查了数轴与有理数,根据点B表示的数,分向左和向右两种情况讨论即可求出答案,明确数轴的特点,分情况讨论是解题的关键
4. (2025·广西南宁期中)如图,一个动点从原点O开始向左运动,每秒运动1个单位长度,并且规定:每向左运动3秒就向右运动2秒,则该动点运动到第2025秒时所对应的数是(
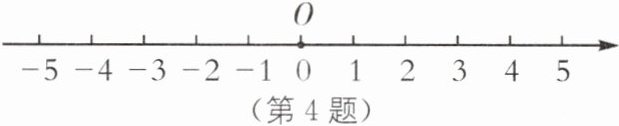
A.-405
B.-406
C.-1010
D.-1011
A
).
A.-405
B.-406
C.-1010
D.-1011
答案:
A [解析]
∵一个动点从原点O开始向左运动,每秒运动1个单位长度,并且规定:每向左运动3秒就向右运动2秒,
∴该点运动周期为5秒,每5秒向左运动1个单位长度;
∵2025÷5=405,
∴该点运动到2025秒时对应的数为−405.故选A.思路引导 根据题意利用运动周期找出规律,解题关键是求出运动周期.
∵一个动点从原点O开始向左运动,每秒运动1个单位长度,并且规定:每向左运动3秒就向右运动2秒,
∴该点运动周期为5秒,每5秒向左运动1个单位长度;
∵2025÷5=405,
∴该点运动到2025秒时对应的数为−405.故选A.思路引导 根据题意利用运动周期找出规律,解题关键是求出运动周期.
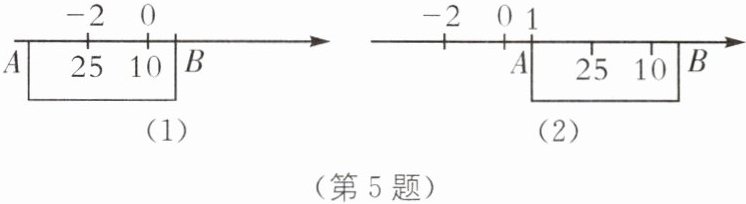
5. (2024·浙江温州期中)刻度尺在数轴上的位置摆放如图(1)所示,刻度尺右端点B的刻度为“0”,刻度“10cm”和“25cm”分别与数轴上表示数0和-2的点重合,现将刻度尺沿数轴向右移动5个单位,如图(2),使刻度尺的左端点A与数轴上表示的数1重合,求刻度尺的长度.

答案:
∵刻度“10cm”和“25cm”分别与数轴上表示数0和−2的点重合,
∴数轴上一个单位长度为(25−10)÷2=7.5(cm).
∵将该刻度尺沿数轴向右平移5个单位,刻度尺的左端点A与数轴上表示的数1重合,
∴原点A表示的数是−4,则点A到原点的距离为4×7.5=30(cm),刻度尺长为30+10=40(cm).思路引导 本题考查了数轴与刻度尺,根据刻度“10cm”和“25cm”分别与数轴上表示的数0和−2的点重合,可求出数轴上一个单位长度是7.5cm,再根据向右平移5个单位得出点A表示的数,就可求出刻度尺的长,解题的关键是求出一个单位长度代表多少厘米.
∵刻度“10cm”和“25cm”分别与数轴上表示数0和−2的点重合,
∴数轴上一个单位长度为(25−10)÷2=7.5(cm).
∵将该刻度尺沿数轴向右平移5个单位,刻度尺的左端点A与数轴上表示的数1重合,
∴原点A表示的数是−4,则点A到原点的距离为4×7.5=30(cm),刻度尺长为30+10=40(cm).思路引导 本题考查了数轴与刻度尺,根据刻度“10cm”和“25cm”分别与数轴上表示的数0和−2的点重合,可求出数轴上一个单位长度是7.5cm,再根据向右平移5个单位得出点A表示的数,就可求出刻度尺的长,解题的关键是求出一个单位长度代表多少厘米.
6. (2025·黑龙江哈尔滨呼兰期末)兰兰早晨骑自行车,她从自己家出发,向东骑行1km到达迎迎家,继续向东骑行3.5km到达欢欢家,然后又向西骑行了6.5km到达学校,最后又向东骑行回到自己家.
(1)若以兰兰家为原点,向东的方向为正方向,用1个单位长度表示1km,分别用点A,B,C表示出迎迎家、欢欢家、学校的位置.
(2)迎迎家与学校之间的距离为______km.
(3)如果兰兰骑行的速度是每分钟200米,那么兰兰从出发骑行到学校一共用了多长时间?
(1)若以兰兰家为原点,向东的方向为正方向,用1个单位长度表示1km,分别用点A,B,C表示出迎迎家、欢欢家、学校的位置.
(2)迎迎家与学校之间的距离为______km.
(3)如果兰兰骑行的速度是每分钟200米,那么兰兰从出发骑行到学校一共用了多长时间?
答案:
(1)如图所示:
(2)3
(3)200米/分钟=0.2千米/分钟,(1+3.5+6.5)÷0.2=11÷0.2=55(分钟).故兰兰从出发骑行到学校一共用了55分钟.
(1)如图所示:

(2)3
(3)200米/分钟=0.2千米/分钟,(1+3.5+6.5)÷0.2=11÷0.2=55(分钟).故兰兰从出发骑行到学校一共用了55分钟.
7. (2025·浙江金华期中)已知点C是线段AB上的一个点,若点C到线段两个端点的距离之比为1:2时,则称点C为线段AB的“理想点”.如图(1),A,B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
(1)求点A,B之间的距离.
(2)求线段AB的“理想点”C所对应的数.

(1)求点A,B之间的距离.
(2)求线段AB的“理想点”C所对应的数.

答案:
(1)
∵A点对应的数为−20,B点对应的数为100,
∴点A,B之间的距离是120.
(2)
∵AB=120,点C到线段两个端点的距离之比为1:2,当AC:CB=1:2时,AC=$\frac{1}{3}$×120=40,
∵A点对应的数为−20,
∴C点所对应的数为20;当AC:CB=2:1时,AC=$\frac{2}{3}$×120=80,
∵A点对应的数为−20,
∴C点所对应的数为60.
∴线段AB的“理想点”C所对应的数是20或60.思路引导 本题考查数轴上两点之间的距离和翻折问题,理解题意,分类讨论是解题的关键.
(1)根据数轴上两点之间的距离定义求解即可.
(2)根据“理想点”定义及C到A,B距离的比例关系,分情况讨论C对应数轴上的数即可.
(1)
∵A点对应的数为−20,B点对应的数为100,
∴点A,B之间的距离是120.
(2)
∵AB=120,点C到线段两个端点的距离之比为1:2,当AC:CB=1:2时,AC=$\frac{1}{3}$×120=40,
∵A点对应的数为−20,
∴C点所对应的数为20;当AC:CB=2:1时,AC=$\frac{2}{3}$×120=80,
∵A点对应的数为−20,
∴C点所对应的数为60.
∴线段AB的“理想点”C所对应的数是20或60.思路引导 本题考查数轴上两点之间的距离和翻折问题,理解题意,分类讨论是解题的关键.
(1)根据数轴上两点之间的距离定义求解即可.
(2)根据“理想点”定义及C到A,B距离的比例关系,分情况讨论C对应数轴上的数即可.
查看更多完整答案,请扫码查看


