《2025年实验班提优训练七年级数学上册人教版》

1. (2024·兰州中考)2024 的绝对值是(B)。
A.-2024
B.2024
C.$\frac{1}{2024}$
D.$-\frac{1}{2024}$

答案： B

2. (2024·成都中考)-5 的绝对值是(A)。
A.5
B.-5
C.$\frac{1}{5}$
D.$-\frac{1}{5}$

答案： A [解析]根据负数的绝对值等于它的相反数，得|−5| = 5.故选A
归纳总结　本题考查绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.

3. (2025·湖南长沙宁乡期末)若一个数的绝对值是 2,则这个数是(C)。
A.2
B.-2
C.±2
D.0

答案： C [解析]一个数的绝对值是2,即在数轴上表示这个数的点到原点的距离为2，所以这个数是2或−2.故选C.

4. 如果 $a$ 是有理数,那么 $|a| + 2025$ 的最小值是2025。

答案： 2025 [解析]
∵|a|≥0,
∴|a|+2025≥2025,
∴|a|+2025的最小值是2025.

5. (教材 P14 练习 T3·变式)如果 $|-x| = \left|-\frac{3}{4}\right|$,那么 $x = $±$\frac{3}{4}$。

答案： ±$\frac{3}{4}$ [解析]
∵|−x| = |−$\frac{3}{4}$|,即|x| = $\frac{3}{4}$,
∴x = ±$\frac{3}{4}$.

6. 写出下列各数的绝对值：
3,-7,-2.1,$\frac{2}{3}$,$-\frac{5}{11}$,0,20。

答案： 3的绝对值是3,−7的绝对值是7,−2.1的绝对值是2.1,$\frac{2}{3}$的绝对值是$\frac{2}{3}$,−$\frac{5}{11}$的绝对值是$\frac{5}{11}$,0的绝对值是0,20的绝对值是20.

7. (2025·河南洛阳期末)古筝是中国独特的民族乐器之一,为了保持音准,弹奏者常使用调音器对每根琴弦进行调音。如图所示是某古筝调音器软件的界面,指针指向 40 表示音调偏高,需放松琴弦。下列指针指向的数字中表示需拧紧琴弦,且最接近标准音(指针指在 0 处为标准音)的是(B)。

A.-20
B.-5
C.10
D.20

答案： B [解析]
∵|−5|＜|10|＜|−20| = |20|,需拧紧琴弦,则该数字为负数，
∴指针指向−5最接近标准音.故选B.

8. (2024·广东湛江期末)下列计算结果为 3 的是(C)。
A.$-|+3|$
B.$+(-3)$
C.$-(-3)$
D.$-|-3|$

答案： C [解析]A.−|+3| = −3,故选项A不符合题意;
B.+(−3) = −3,故选项B不符合题意;
C.−(−3) = 3,故选项C符合题意;
D.−|−3| = −3,故选项D不符合题意.故选C.

9. (2024·广东茂名高州期末)用符号语言表述“正数的绝对值等于它本身”,正确的是(A)。
A.$|a| = a(a ＞ 0)$
B.$|a| = a(a ＜ 0)$
C.$|a| = -a(a \geq 0)$
D.$|a| = -a(a \leq 0)$

答案： A [解析]用符号语言表述“正数的绝对值等于它本身”，正确的是|a| = a(a＞0).故选A.

10. 下列说法正确的是(A)。
A.互为相反数的两个数的绝对值相等
B.绝对值等于本身的数只有正数
C.不相等的两个数绝对值也不相等
D.绝对值相等的两数一定相等

答案： A [解析]A.互为相反数的两个数的绝对值相等，所以A选项正确;
B.绝对值等于本身的数有正数或0,所以B选项错误;
C.不相等的两个数绝对值可能相等,如2与−2.所以C选项错误;
D.绝对值相等的两个数不一定相等，如2与−2,所以D选项错误.故选A.

11. (2025·上海松江区期末)已知 $a$,$b$ 是有理数,$|a| = -a$,$|b| = b$,且 $|a| ＞ |b| ＞ 0$,用数轴上的点来表示 $a$,$b$,正确的是( )。

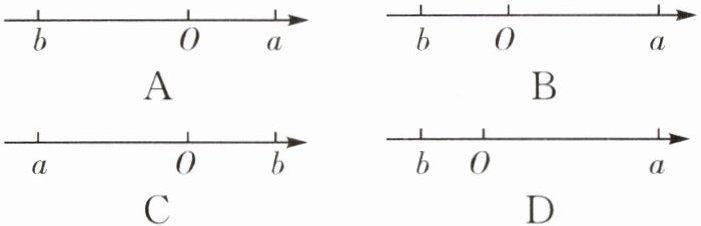
答案：
C [解析]由于|a| = −a,|b| = b,即a为非正数,b为非负数,
∵|a|＞|b|＞0,
∴a＜0,b＞0,且|a|＞|b|.
在数轴上表示a,b大致如图:

故选C;
知识拓展　本题主要考查了绝对值的含义和求法，解答本题的关键是要明确:①当a是正有理数时，a的绝对值是它本身a;②当a是负有理数时，a的绝对值是它的相反数−a;③当a是零时，a的绝对值是零.

12. (教材 P17 习题 T9·变式)若 $m$ 为有理数,则下列四个数中一定为非负数的是(C)。
A.$m$
B.$-m$
C.$|-m|$
D.$-|-m|$

答案： C [解析]m为有理数，即m可以为负数，故A排除;当m为正数时，−m为负数，则B排除;不论m取何值，|−m|一定为非负数，故C正确;不论m取何值，−|−m|一定为非正数，故D排除.故选C.

13. (2025·广东深圳期中)使等式 $|6 + x| = |6| + |x|$ 成立的有理数 $x$ 是(B)。
A.任意一个整数
B.任意一个非负数
C.任意一个非正数
D.任意一个有理数

答案： B [解析]
∵|6 + x| = |6| + |x|,
∴6与x同号或x为0,
∴x是任意一个非负数.故选B