《2025年实验班提优训练七年级数学上册人教版》

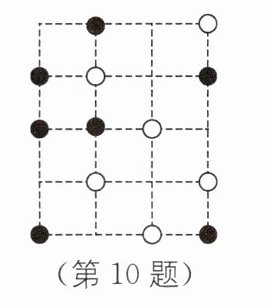
10. 如图,棋盘上有黑、白两色棋子若干,若直线 $ l $ 经过 3 枚颜色相同的棋子,则这样的直线共有____条.

答案：
10.3　[解析]如图，经过3枚颜色相同的棋子的直线共有3条。
　　　　　　　　

11. 数形结合思想 [观察思考]如图,线段 $ AB $ 上有两个点 $ C $,$ D $,分别以点 $ A $,$ B $,$ C $,$ D $ 为端点的线段共有6条.
[模型构建]若线段上有 $ m $ 个点(包括端点),则该线段上共有$\frac{1}{2}m(m-1)$条线段.
[拓展应用]若有 8 位同学参加班级的演讲比赛,比赛采用单循环制(即每两位同学之间都要进行一场比赛),请你应用上述模型构建,求一共要进行多少场比赛.

把8位同学看作线段上的8个点，每两位同学之间的一场比赛看作一条线段，由题意，得当$m=8$时，$\frac{m(m-1)}{2}=\frac{8×(8-1)}{2}=28$。故一共要进行28场比赛。

答案： 11.[观察思考]6
[模型构建]$\frac{1}{2}m(m-1)$
[拓展应用]把8位同学看作线段上的8个点，每两位同学之间的一场比赛看作一条线段，由题意，得当$m=8$时，$\frac{m(m-1)}{2}=\frac{8×(8-1)}{2}=28$。故一共要进行28场比赛。
易错警示　本题主要考查了线段的计数问题，解本题的关键是找出规律，此类题目容易数重或遗漏，要特别注意。

12. 归纳法(2025·广东深圳期末)阅读以下材料并填空.
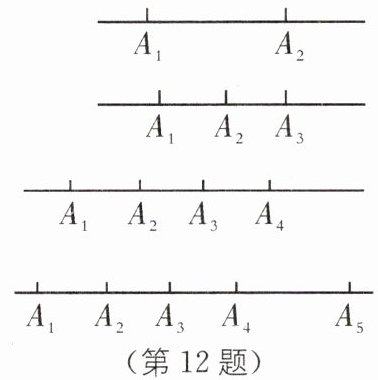
[问题]在一条直线上有 $ n $ 个点($ n \geqslant 2 $),每两个点确定一条线段,一共有多少条线段？
[探究]当仅有 2 个点时,有 $ \frac{1 × 2}{2} = 1 $ 条线段；
当有 3 个点时,有 $ \frac{2 × 3}{2} = 3 $ 条线段；
当有 4 个点时,有 $ \frac{3 × 4}{2} = 6 $ 条线段；
当有 5 个点时,有$\frac{4×5}{2}=10$条线段；
…
当有 $ n $ 个点时,从这些点中任意取一点,如图,以这个点为端点和其余各点能组成 $ (n - 1) $ 条线段,这样总共有 $ n(n - 1) $ 条线段. 在这些线段中每条线段都重复了两次,如：线段 $ A_1A_2 $ 和 $ A_2A_1 $ 是同一条线段,所以,一条直线上有 $ n $ 个点,一共有$\frac{n(n-1)}{2}$条线段.
[应用]
(1)在一条直线上有 10 个点,直线外一点分别与这 10 个点连接成线段,一共可以组成45个三角形.
(2)平面上有 50 个点,且任意三个点不在同一直线上,过这些点作直线,一共能作出1225条不同的直线.
[拓展]平面上有 $ n(n \geqslant 3) $ 个点,任意三个点不在同一直线上,过任意三点作三角形,一共能作出多少个不同的三角形？

答案： 12.[探究]$\frac{4×5}{2}=10$ $\frac{n(n-1)}{2}$
[应用]
(1)45　[解析]
∵当$n=10$时，$\frac{10×(10-1)}{2}=45$，
∴一共可以组成45个三角形。
(2)1225　[解析]
∵当$n=50$时，$\frac{50×(50-1)}{2}=1225$，
∴一共能作出1225条不同的直线。
[拓展]当有3个点时，可作1个三角形，$1=\frac{3×2×1}{6}$；当有4个点时，可作4个三角形，$4=\frac{4×3×2}{6}$；当有5个点时，可作10个三角形，$10=\frac{5×4×3}{6}$；…当有n个点时，可连成$\frac{n(n-1)(n-2)}{6}$个三角形。
素养考向　本题考查了图形的变化类规律探究，关键是通过归纳与总结，得到其中的规律，并用得到的规律解题。体现了由特殊到一般，并由一般到特殊的方法。