第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1. $7+(-3)+(-4)+18+(-11)= (7+18)+[(-3)+(-4)+(-11)]$是应用了(
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与结合律
D
)A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与结合律
答案:
D [解析]7+(−3)+(−4)+18+(−11)=(7+18)+[(−3)+(−4)+(−11)]是应用了加法交换律与结合律.故选D.
2. 运用加法的运算律计算$(+6\frac {1}{3})+(-18)+4\frac {2}{3}+(-6.8)+18+(-3.2)$,最适当的是(
A.$[(+6\frac {1}{3})+4\frac {2}{3}+18]+[(-18)+(-6.8)+(-3.2)]$
B.$[(+6\frac {1}{3})+(-6.8)+4\frac {2}{3}]+[(-18)+18+(-3.2)]$
C.$[(+6\frac {1}{3})+(-18)+4\frac {2}{3}]+(-6.8)+[18+(-3.2)]$
D.$[(+6\frac {1}{3})+4\frac {2}{3}]+[(-18)+18]+[(-6.8)+(-3.2)]$
D
).A.$[(+6\frac {1}{3})+4\frac {2}{3}+18]+[(-18)+(-6.8)+(-3.2)]$
B.$[(+6\frac {1}{3})+(-6.8)+4\frac {2}{3}]+[(-18)+18+(-3.2)]$
C.$[(+6\frac {1}{3})+(-18)+4\frac {2}{3}]+(-6.8)+[18+(-3.2)]$
D.$[(+6\frac {1}{3})+4\frac {2}{3}]+[(-18)+18]+[(-6.8)+(-3.2)]$
答案:
D [解析](+6$\frac{1}{3}$)+(−18)+4$\frac{2}{3}$+(−6.8)+18+(−3.2)=[(+6$\frac{1}{3}$)+4$\frac{2}{3}$]+[(−18)+18]+[(−6.8)+(−3.2)].故选D.
3. 教材P29例2·变式 用适当方法计算:
(1) $(-51)+(+12)+(-7)+(-11)+(+36)$;
(2) $(-4\frac {5}{8})+7.75+(-1\frac {3}{8})+(-2\frac {3}{4})$;
(3) $1.3+0.5+(-0.5)+0.3+(-0.7)+3.2+(-0.3)+0.7$.
(1) $(-51)+(+12)+(-7)+(-11)+(+36)$;
(2) $(-4\frac {5}{8})+7.75+(-1\frac {3}{8})+(-2\frac {3}{4})$;
(3) $1.3+0.5+(-0.5)+0.3+(-0.7)+3.2+(-0.3)+0.7$.
答案:
(1)(−51)+(+12)+(−7)+(−11)+(+36)=[(−51)+(−7)+(−11)]+[(+12)+(+36)]=(−69)+48 = −21.
(2)(−4$\frac{5}{8}$)+7.75+(−1$\frac{3}{8}$)+(−2$\frac{3}{4}$)=[(−4$\frac{5}{8}$)+(−1$\frac{3}{8}$)]+[7.75+(−2$\frac{3}{4}$)]=−6 + 5 = −1.
(3)1.3+0.5+(−0.5)+0.3+(−0.7)+3.2+(−0.3)+0.7=(1.3+3.2)+[0.5+(−0.5)]+[0.3+(−0.3)]+[(−0.7)+0.7]=4.5+0 = 4.5.
思路引导 本题考查有理数的加法运算,掌握运算法则是解题的关键,运用加法交换律和加法结合律可简化计算.
(1)(−51)+(+12)+(−7)+(−11)+(+36)=[(−51)+(−7)+(−11)]+[(+12)+(+36)]=(−69)+48 = −21.
(2)(−4$\frac{5}{8}$)+7.75+(−1$\frac{3}{8}$)+(−2$\frac{3}{4}$)=[(−4$\frac{5}{8}$)+(−1$\frac{3}{8}$)]+[7.75+(−2$\frac{3}{4}$)]=−6 + 5 = −1.
(3)1.3+0.5+(−0.5)+0.3+(−0.7)+3.2+(−0.3)+0.7=(1.3+3.2)+[0.5+(−0.5)]+[0.3+(−0.3)]+[(−0.7)+0.7]=4.5+0 = 4.5.
思路引导 本题考查有理数的加法运算,掌握运算法则是解题的关键,运用加法交换律和加法结合律可简化计算.
4. (2025·福建三明期中)若$\frac {2}{3}+(-2.5)+3.5+(-\frac {2}{3})= [\frac {2}{3}+(-\frac {2}{3})]+[(-2.5)+3.5]$,则这个算式(
A.只用了加法交换律
B.只用了加法结合律
C.既用了加法交换律,又用了加法结合律
D.没有运用运算律
C
).A.只用了加法交换律
B.只用了加法结合律
C.既用了加法交换律,又用了加法结合律
D.没有运用运算律
答案:
C [解析]根据题意可知,等式中第四项与第二项带着符号交换位置,运用了加法交换律,第一项与交换后的第二项结合,交换后的第三项与第四项结合,运用了加法结合律.故选C.
5. 新情境 月历数学 (2025·广东广州番禺区期末)如图是某一年1月份的月历.带阴影的框是“7”字型框,设框中的四个数之和为t,平移“7”字型框,则t的最大值为(
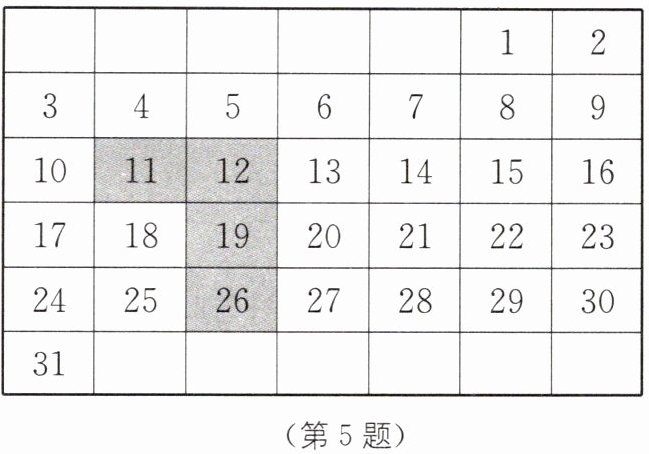
A.92
B.88
C.84
D.80
C
).
A.92
B.88
C.84
D.80
答案:
C [解析]观察月历表,可得出当t最大时,“7”字型框框住的四个数分别为15,16,23,30.
∵15+16+23+30 = 84,
∴t的最大值为84.故选C.
∵15+16+23+30 = 84,
∴t的最大值为84.故选C.
查看更多完整答案,请扫码查看


