《2025年实验班提优训练七年级数学上册人教版》

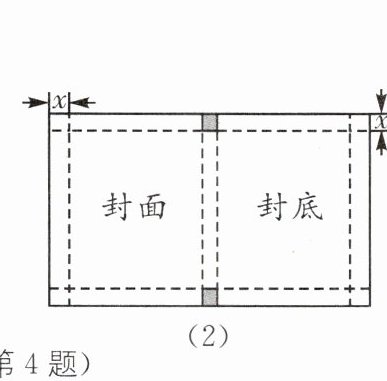
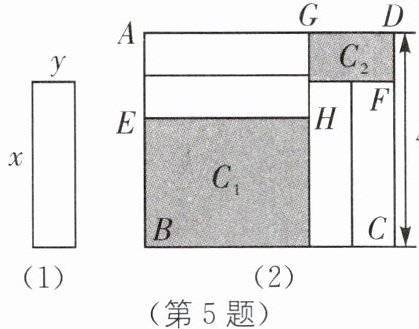
5. (2025·石家庄裕华区一模)将4个如图(1)所示的长为$x$,宽为$y(x＞y)$的小长方形按照图(2)的方式不重叠地摆放在大长方形$ABCD$中,$CD= 4$,大长方形$ABCD中未被覆盖的两部分分别记为C_1和C_2$.
(1)求图形$C_2$的周长(用含$x,y$的式子表示).
(2)要求图形$C_1和C_2$的周长和,嘉嘉认为必须告诉$x,y$的值;淇淇认为不用告诉$x,y$的值,你认为谁的看法正确? 请说明理由.

答案： 5.
(1)由题图可知,图形$C_{2}$的长$DG=2y$,宽$DF=4-x$,$\therefore$图形$C_{2}$的周长为$2(DG+DF)=2(2y+4-x)=4y-2x+8$.
(2)淇淇的看法正确,理由如下:$\because$由题图可知,图形$C_{1}$的周长为$2(EH+BE)$,图形$C_{2}$的周长为$2(DG+DF)$,且$EH+DG=BC$,$\therefore$图形$C_{1}$和$C_{2}$的周长和为$2(EH+BE+DG+DF)=2(BC+BE+DF)=2(x+2y+4-2y+4-x)=16$,$\therefore$淇淇的看法正确.
归纳总结 本题主要考查代数式、整式的加减运算与图形周长的计算,理解图形,掌握整式的加减运算法则是解题的关键.

6. (1)探索:如图(1),在边长为$x$的正方形纸片的4个角都剪去1个边长是$a$的正方形.试用含$a,x$的式子表示纸片剩余部分的面积为$x^{2}-4a^{2}$;
(2)变式:如图(2),在边长为$x$的正方形纸片的4个角都剪去一个相同的扇形,扇形的半径为$r$,用$r,a$表示纸片剩余部分的面积为$x^{2}-πr^{2}$,剩余部分图形的周长为$4x-8r+2πr$;
(3)拓展:世博会中国国家馆模型的平面图如图(3)所示,其外框是一个大正方形,中间四个全等的小正方形(阴影部分)是支撑展馆的核心筒,标记字母的五个全等的正方形是展厅,展厅的边长为$m$,已知核心筒的边长比展厅的边长的一半多1米,用含有$m$的式子表示外框的边长.外框的边长为$3m+2×(\frac {1}{2}m+1)=4m+2$.

答案： 6.
(1)$x^{2}-4a^{2}$
(2)$x^{2}-πr^{2}$ $4x-8r+2πr$
(3)外框的边长为$3m+2×(\frac {1}{2}m+1)=4m+2$.