《2025年实验班提优训练七年级数学上册人教版》

15. (2025·山东聊城茌平区期中)有理数 a,b 在数轴上对应点的位置如图所示.
(1)在数轴上分别用 A,B 两点表示 -a,-b.
(2)若数 b 与 -b 表示的点相距 20 个单位长度,则 b 与 -b 分别是什么?
(3)在(2)的条件下,若数 a 表示的点与数 b 的相反数表示的点相距 5 个单位长度,则 a 与 -a 分别是多少?

答案：

(1)如图：

(2)
∵数b与其相反数表示的点相距20个单位长度,
∴数b表示的点到原点的距离为20÷2=10,
∴b是-10,-b是10.
(3)
∵数-b表示的点到原点的距离为10,而数a表示的点与数b的相反数表示的点相距5个单位长度,且数a表示的点在数-b表示的点的左边,
∴数a表示的点到原点的距离为10-5=5,
∴a是5,-a是-5.

16. 归纳法 (2025·内蒙古巴彦淖尔期中改编)化简下列各式的符号,并回答问题:
(1)$-(-2)=$2;$+(-\frac{1}{3})=$$-\frac{1}{3}$;$-[-(-5)]=$-5;$-[-(+4.5)]=$4.5;$-[-(+6)]=$6.
(2)当 +5 前面有 99 个负号时,化简后的结果是-5;当 -5 前面有 100 个负号时,化简后的结果是5;你能总结出什么规律?
(3)计算:$-\underbrace{\{-\left[ \cdots -(-3) \right]\}}_{2n个负号,n是正整数}+\underbrace{\left\{ -\left[ \cdots -(-1) \right] \right\}}_{(2n-1)个负号,n是正整数}=3-1=2$

答案：
(1)2 $-\frac{1}{3}$ -5 4.5 6
(2)-5 5 [解析]①当+5前面有99个负号时,化简后结果是-5.
②当-5前面有100个负号时,化简后结果是-5.
总结规律:一个数的前面有奇数个负号,化简后的结果等于它的相反数,有偶数个负号,化简后的结果等于它本身.
(3)$-\underbrace{\{-\left[ \cdots -(-3) \right]\}}_{2n个负号,n是正整数}+\underbrace{\left\{ -\left[ \cdots -(-1) \right] \right\}}_{(2n-1)个负号,n是正整数}=3-1=2$.
归纳总结 本题考查了规律型:数字的变化类,利用相反数的定义化简,熟记概念并仔细观察化简结果与负号的关系是解题的关键.

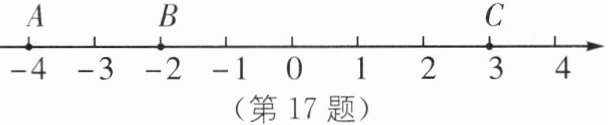
17. 中考新考法 满足结论的条件开放 如图,在数轴上有三个点 A,B,C,请据图回答下列问题:
(1)将点 B 向左移动 3 个单位长度后,三个点所表示的数谁最小? 是多少?
(2)怎样移动 A,B 两点中的一个,才能使这两个点所表示的数互为相反数? 有几种移动方法?
(3)怎样移动 A,B,C 三点中的两个点,才能使三个点所表示的数相同? 有几种移动方法?

答案：
(1)将点B向左平移3个单位长度后,点B所表示的数最小,是-5.
(2)有两种移动方法:①点A不动,点B右移6个单位长度;②点B不动,点A右移6个单位长度.
(3)有三种移动方法:①点A不动,把点B左移2个单位长度,点C左移7个单位长度;②点B不动,把点A右移2个单位长度,点C左移5个单位长度;③点C不动,把点A右移7个单位长度,点B右移5个单位长度.