《2025年实验班提优训练七年级数学上册人教版》

1. (2024·湖北武汉江汉区期中)已知$x - 2y = - 5$,则$2 - x + 2y$的值是(D).
A.0
B.2
C.-3
D.7

答案： 1.D [解析]
∵x-2y=-5,
∴2-x+2y=2-(x-2y)=2+5=7.故选D.

2. 如果代数式$a^{2} - 2b + 1$的值为3,那么代数式$8 - a^{2} + 2b$的值等于6.

答案： 2.6 [解析]
∵a²-2b+1=3,
∴a²-2b=2,
∴8-a²+2b=8-(a²-2b)=8-2=6.

3. 若二次三项式$2x^{2} - 6x + 4$的值为10,则$x^{2} - 3x - 2024$的值为(D).
A.2019
B.2021
C.-2019
D.-2021

答案： 3.D [解析]
∵二次三项式2x²-6x+4的值为10,
∴2x²-6x+4=10,
∴x²-3x=3,
∴x²-3x-2024=3-2024=-2021.故选D.
思路引导 本题考查了代数式求值.整体代入是解题的关键.由题意知,2x²-6x+4=10,则x²-3x=3,然后整体代入求解即可.

4. 已知$A = x^{2} + xy - 2x - 3$,$B = - x^{2} + 3xy - 9$. 若$3A - B$的值等于-2,则代数式$x^{2} - \frac{3}{2}x + 3$的值是$\frac{5}{2}$.

答案： 4.$\frac{5}{2}$ [解析]
∵A=x²+xy-2x-3,B=-x²+3xy-9,
∴3A-B=3(x²+xy-2x-3)-(-x²+3xy-9)=3x²+3xy-6x-9+x²-3xy+9=4x²-6x=-2,即2x²-3x=-1.
∴x²-$\frac{3}{2}$x+3=$\frac{1}{2}$(2x²-3x)+3=$\frac{1}{2}$×(-1)+3=$\frac{5}{2}$.

5. (2024·安徽蚌埠蚌山区期末)如果代数式$a^{2} - 3a + 7$的值为8,那么代数式$7 - 2a^{2} + 6a$的值为(B).
A.8
B.5
C.-8
D.-5

答案： 5.B [解析]
∵代数式a²-3a+7的值为8,
∴a²-3a=1,
∴7-2a²+6a=7-2(a²-3a)=7-2×1=5.故选B.

6. 若$m^{2} - 2n = - 1$,则代数式$3m^{2} - 6n + 2$的值为-1.

答案： 6.-1 [解析]
∵m²-2n=-1,
∴3m²-6n+2=3(m²-2n)+2=3×(-1)+2=-1.

7. 已知$x^{2} - 2y - 4 = 0$,则多项式$- 2x^{2} + 4y - 6$的值为-14.

答案： 7.-14 [解析]
∵x²-2y-4=0,
∴x²-2y=4,
∴-2x²+4y=-8,
∴-2x²+4y-6=-8-6=-14.

8. (2024·甘孜州中考)若$x^{2} + 2x = 3$,则$2x^{2} + 4x - 5 = $1.

答案： 8.1 [解析]
∵x²+2x=3,
∴2x²+4x-5=2(x²+2x)-5=2×3-5=6-5=1.

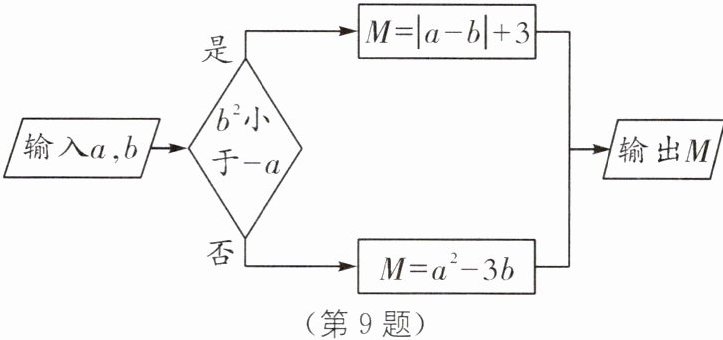
9. (2024·北京东城区期末)小明设计了一个如图所示的数值转换程序.
(1)当输入$a = - 5$,$b = - 3$时,输出$M$的值为多少?
(2)若$a = - 3$,$M$的值大于4,直接写出一个符合条件的$b$的值.

答案： 9.
(1)由题意知,b²=9,-a=5,
∴b²＞-a,
∴M=a²-3b=(-5)²-3×(-3)=34,
∴输出M的值为34.
(2)由题意,知-a=3,当b=1时,b²=1,且b²＜-a,
∴M=|a-b|+3=|-3-1|+3=7＞4,
∴b=1符合条件.(答案不唯一)

10. (2025·河北张家口期中)在数学课上,老师给出了一道题目：“先化简,再求值：$(2x^{2} + □ x - 1) - 4(\frac{1}{2}x^{2} + 2x + 7)$,其中$x = - | - 2 |$. ”“$□$”中的数据被污染,无法解答,只记得“$□$”中是一个有理数,于是老师即兴出题,请同学们回答.
(1)请直接写出化简后整式的常数项是多少?
(2)若嘉嘉把“$x = - | - 2 |$”看成了“$x = | - 2 |$”,化简求值的结果仍不变,求此时“$□$”表示的有理数.
(3)若淇淇把“$x = - | - 2 |$”看成了“$x = - ( - 2)$”,化简求值的结果为-5,求当$x = - | - 2 |$时,原整式的值.

答案： 10.
(1)设□中的数据为a,(2x²+□x-1)-4($\frac{1}{2}$x²+2x+7)=2x²+ax-1-2x²-8x-28=(a-8)x-29,化简后的代数式中常数项是-29.
(2)设“□”表示的有理数的值为a.原式=(a-8)x-29.因为把“x=-|-2|”看成了“x=|-2|”,化简求值的结果仍不变,即原式的值与x的值无关,所以a-8=0,解得a=8,所以“□”表示的有理数为8.
(3)设“□”表示的有理数的值为a.原式=(a-8)x-29.因为当x=-(-2)时,化简求值的结果为-5,所以(a-8)×2-29=-5,解得a=20,所以原式=(20-8)×(-2)-29=-53.