《2025年实验班提优训练七年级数学上册人教版》

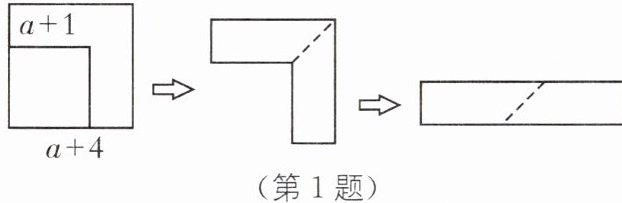
1. (2024·河北唐山十二中期中改编)如图,从边长为$(a+4)的大正方形纸片中剪去一个边长为(a+1)的小正方形(a＞0)$,剩余部分沿虚线剪开,拼成一个长方形(不重叠无缝隙),则长方形的面积为(B).

A.$a(2a+5)$
B.$3(2a+5)$
C.$3(2a+1)$
D.$a(2a+1)$

答案： 1.B [解析]由图可知,长方形的宽为$(a+4)-(a+1)=3$,长为$(a+4)+(a+1)=2a+5$.$\therefore$长方形的面积为$3(2a+5)$.故选 B.

2. (2025·陕西榆林榆阳区期末)根据素材,解决下列问题

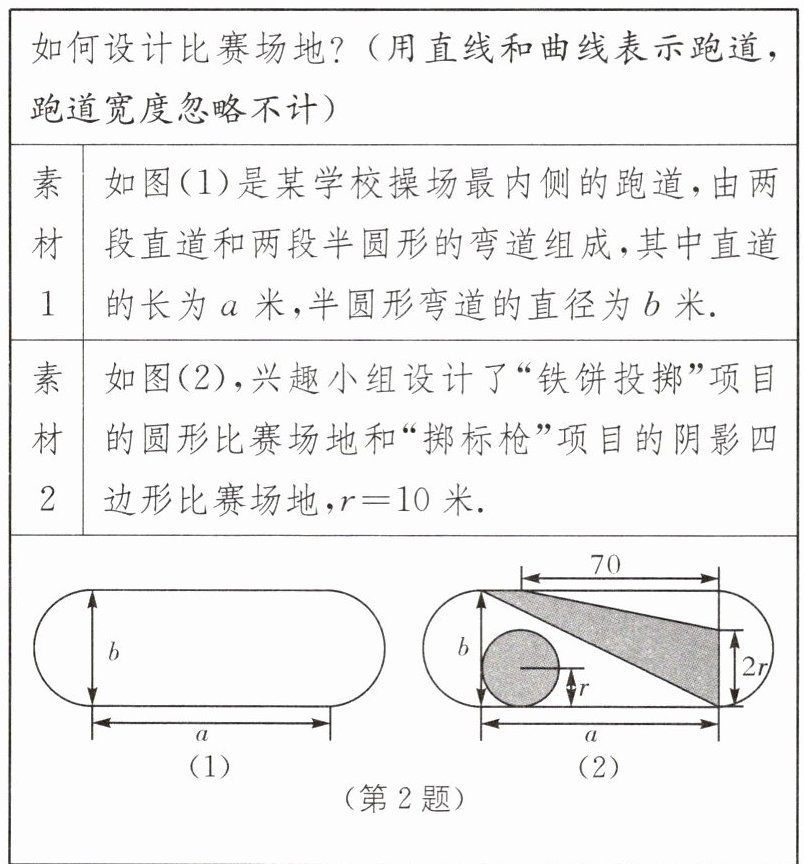
(1)用含$a,b,r的代数式表示两项比赛场地的总面积S$(阴影部分面积的和);
$S=πr^{2}+\frac {1}{2}ab-35b+70r$
(2)若$a= 80,b= 40$,求$S$的值($\pi$取3).
1200平方米

答案： 2.
(1)$S=πr^{2}+\frac {1}{2}ab-\frac {1}{2}×(b-2r)×70=πr^{2}+\frac {1}{2}ab-35b+70r$.
(2)将$a= 80,b= 40,r=10$代入,得$S=πr^{2}+\frac {1}{2}ab-35b+70r=3×10^{2}+\frac {1}{2}×80×40-35×40+70×10=1200$(平方米).
归纳总结 本题主要考查了整式的加减运算、代数式求值,含乘方的有理数混合运算,熟练掌握含乘方的有理数混合运算法则是解题的关键.

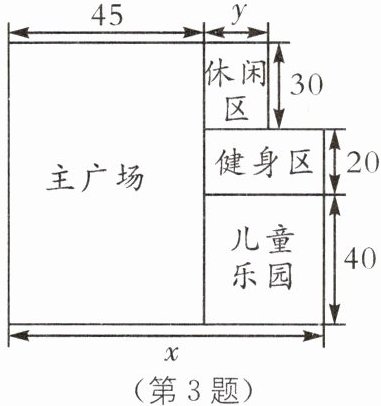
3. (2025·安徽合肥高新区期中)某地为居民打造十五分钟健身圈,计划将一块闲置土地改造成一个休闲广场(由主广场、儿童乐园区、健身区和休闲区组成),现对该地块进行地面改造,其平面图如图所示(单位:米).
(1)用含$x,y$的代数式表示儿童乐园区比休闲区面积大多少平方米?
(2)用含$x,y$的代数式表示该休闲广场的总面积.
(3)该休闲广场地面全部铺设地砖,但为了确保安全,还需要在健身区和儿童乐园区的地砖上额外增加一层橡胶地垫.已知每平方米地砖的铺设成本为150元,每平方米橡胶地垫的铺设成本为100元.当$x= 80,y= 15$时,求该休闲广场地面改造的总费用.(不考虑其他额外费用,计算结果使用科学记数法表示)

答案： 3.
(1)$40(x-45)-30y=(40x-30y-1800)$平方米.故用含x,y 的代数式表示儿童乐园区比休闲区面积大$(40x-30y-1800)$平方米.
(2)$(40+20+30)x-30(x-y-45)=(60x+30y+1350)$平方米.故用含x,y 的代数式表示该休闲广场的总面积为$(60x+30y+1350)$平方米.
(3)当$x= 80,y= 15$时,$150×(60x+30y+1350)+100×(40+20)(x-45)=9000x+4500y+202500+6000x-270000=15000x+4500y-67500=15000×80+4500×15-67500=1200000+67500-67500=1200000=1.2×10^{6}$(元).故该休闲广场地面改造的总费用为$1.2×10^{6}$元.

4. 新情境 课本包装 书籍是人类进步的阶梯! 为爱护书本一般都将书本用封皮包好,现有一本数学书籍如图(1)所示,其长为26cm、宽为18.5cm、厚为1cm.小军用一张长方形纸包好了这本数学书,他将封面和封底各折进去$x$cm,封皮展开后如图(2)所示.求:
(1)小军所用的这张包书纸的长是$38+2x$cm,宽是$26+2x$cm.(用含$x$的代数式表示)
(2)当封面和封底各折进去2cm时,请帮小军计算一下他用的长方形包书纸的周长是多少厘米?
根据题意,周长为$2(38+2x)+2(26+2x)=128+8x$,当$x=2$时,$128+8x=128+8×2=144(cm)$.故他所用的长方形包书纸的周长是144 cm.

答案： 4.
(1)$(38+2x)(26+2x)$
(2)根据题意,周长为$2(38+2x)+2(26+2x)=128+8x$,当$x=2$时,$128+8x=128+8×2=144(cm)$.故他所用的长方形包书纸的周长是144 cm.