第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1. (2025·浙江杭州期中)定义新运算:$\begin{vmatrix} a&c\\ b&d\end{vmatrix} = ad-bc$,计算$\begin{vmatrix} -1&2024\\ 0&2027\end{vmatrix} = $
-2027
.
答案:
-2027 [解析]
∵|a c|=ad-bc,
|b d|
∴|-1 2024|=-1×2027-0×2024=-2027-
|0 2027|
0=-2027.
∵|a c|=ad-bc,
|b d|
∴|-1 2024|=-1×2027-0×2024=-2027-
|0 2027|
0=-2027.
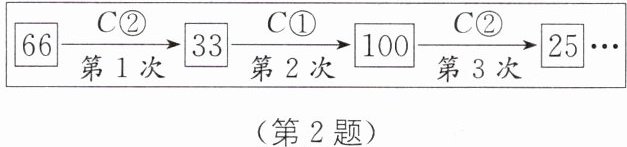
2. 定义一种对正整数$n$的“$C$运算”:①当$n$为奇数时,结果为$3n+1$;②当$n$为偶数时,结果为$\frac {n}{2^{k}}$(其中$k是使\frac {n}{2^{k}}$为奇数的正整数)并且运算重复进行,例如:$n= 66$时,其“$C$运算”如图:
若$n= 26$,则第$2023$次“$C$运算”的结果是(
A.$4$
B.$1$
C.$16$
D.$\frac {3}{2}$
若$n= 26$,则第$2023$次“$C$运算”的结果是(
B
).
A.$4$
B.$1$
C.$16$
D.$\frac {3}{2}$
答案:
B [解析]由题意可得,当n=26时,第一次输出的结果为13,第二次输出的结果为40,第三次输出的结果为5,第四次输出的结果为16,第五次输出的结果为1,第六次输出的结果为4,第七次输出的结果为1,第八次输出的结果为4,…,
∴从第五次开始,奇数次输出的结果为1,偶数次输出的结果为4,
∴第2023次“C运算”的结果是1,故选B.
∴从第五次开始,奇数次输出的结果为1,偶数次输出的结果为4,
∴第2023次“C运算”的结果是1,故选B.
3. (2025·吉林高新区期末)如图所示是计算机程序的计算过程,当输入的数$m为5$时,则输出的结果$n= $
-4
.
答案:
-4 [解析]当m=5时,
∵5>-1,
∴5-2=3.
∵3>-1,
∴3-2=1.
∵1>-1,
∴1-2=-1.
∵-1=-1,
∴-1-2=-3.
∵-3<-1,
∴-(-3)=3,3+(-7)=-4.
∵5>-1,
∴5-2=3.
∵3>-1,
∴3-2=1.
∵1>-1,
∴1-2=-1.
∵-1=-1,
∴-1-2=-3.
∵-3<-1,
∴-(-3)=3,3+(-7)=-4.
4. 中考新考法 规律探究 (2025·上海黄浦区期中)[阅读材料]三千多年前,埃及人发明了一种书写分数的方法,这些分数的分子为$1$,它们被称为“单位分数”,通过探究,小明发现有一些分数,可以很容易地拆分为两个不同的“单位分数”之和(或差).例如:
$\frac {5}{6}= \frac {3+2}{2×3}= \frac {3}{2×3}+\frac {2}{2×3}= \frac {1}{2}+\frac {1}{3},\frac {7}{12}= \frac {4+3}{3×4}= \frac {4}{3×4}+\frac {3}{3×4}= \frac {1}{3}+\frac {1}{4},... ,$
$\frac {1}{6}= \frac {3-2}{2×3}= \frac {3}{2×3}-\frac {2}{2×3}= \frac {1}{2}-\frac {1}{3},\frac {1}{12}= \frac {4-3}{3×4}= \frac {4}{3×4}-\frac {3}{3×4}= \frac {1}{3}-\frac {1}{4},... ;$
(1)请观察小明发现的拆分方法,填空:
①$\frac {9}{20}= \frac {1}{(
②$\frac {1}{20}= \frac {1}{(
(2)请归纳以上拆分规律,计算下列各题:
①$\frac {3}{2}-\frac {5}{6}+\frac {7}{12}-\frac {9}{20}+\frac {11}{30}-\frac {13}{42};$
②$\frac {1}{2}+\frac {1}{6}+\frac {1}{12}+\frac {1}{20}+... +\frac {1}{72}+\frac {1}{90}.$
(3)请运用以上拆分规律,直接写出下列算式的结果:
$\frac {1}{3}+\frac {1}{15}+\frac {1}{35}+\frac {1}{63}+\frac {1}{99}= $
$\frac {1}{3}-\frac {2}{15}+\frac {3}{35}-\frac {4}{63}+\frac {5}{99}= $
$\frac {5}{6}= \frac {3+2}{2×3}= \frac {3}{2×3}+\frac {2}{2×3}= \frac {1}{2}+\frac {1}{3},\frac {7}{12}= \frac {4+3}{3×4}= \frac {4}{3×4}+\frac {3}{3×4}= \frac {1}{3}+\frac {1}{4},... ,$
$\frac {1}{6}= \frac {3-2}{2×3}= \frac {3}{2×3}-\frac {2}{2×3}= \frac {1}{2}-\frac {1}{3},\frac {1}{12}= \frac {4-3}{3×4}= \frac {4}{3×4}-\frac {3}{3×4}= \frac {1}{3}-\frac {1}{4},... ;$
(1)请观察小明发现的拆分方法,填空:
①$\frac {9}{20}= \frac {1}{(
4
)}+\frac {1}{( 5
)};$②$\frac {1}{20}= \frac {1}{(
4
)}-\frac {1}{( 5
)}.$(2)请归纳以上拆分规律,计算下列各题:
①$\frac {3}{2}-\frac {5}{6}+\frac {7}{12}-\frac {9}{20}+\frac {11}{30}-\frac {13}{42};$
②$\frac {1}{2}+\frac {1}{6}+\frac {1}{12}+\frac {1}{20}+... +\frac {1}{72}+\frac {1}{90}.$
(3)请运用以上拆分规律,直接写出下列算式的结果:
$\frac {1}{3}+\frac {1}{15}+\frac {1}{35}+\frac {1}{63}+\frac {1}{99}= $
$\frac{5}{11}$
;$\frac {1}{3}-\frac {2}{15}+\frac {3}{35}-\frac {4}{63}+\frac {5}{99}= $
$\frac{3}{11}$
.
答案:
(1)①4 5 ②4 5
(2)①$\frac{3}{2}-\frac{5}{6}+\frac{7}{12}-\frac{9}{20}+\frac{11}{30}-\frac{13}{42}=(1+\frac{1}{2})-(\frac{1}{2}+\frac{1}{3})+(\frac{1}{3}+\frac{1}{4})-(\frac{1}{4}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{6})-(\frac{1}{6}+\frac{1}{7})=1+\frac{1}{2}-\frac{1}{2}-\frac{1}{3}+\frac{1}{3}+\frac{1}{4}-\frac{1}{4}-\frac{1}{5}+\frac{1}{5}+\frac{1}{6}-\frac{1}{6}-\frac{1}{7}=1-\frac{1}{7}=\frac{6}{7}$.
②$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\cdots+\frac{1}{72}+\frac{1}{90}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}=1-\frac{1}{10}=\frac{9}{10}$.
(3)$\frac{5}{11}$ $\frac{3}{11}$ [解析]$\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+\frac{1}{63}+\frac{1}{99}=\frac{1}{2}×(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{9}-\frac{1}{11})=\frac{1}{2}×(1-\frac{1}{11})=\frac{1}{2}×\frac{10}{11}=\frac{5}{11}$; $\frac{1}{3}-\frac{2}{15}+\frac{3}{35}-\frac{4}{63}+\frac{5}{99}=\frac{1}{4}×[(1+\frac{1}{3})-(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})-(\frac{1}{7}+\frac{1}{9})+(\frac{1}{9}+\frac{1}{11})]=\frac{1}{4}×(1+\frac{1}{11})=\frac{1}{4}×\frac{12}{11}=\frac{3}{11}$.
(1)①4 5 ②4 5
(2)①$\frac{3}{2}-\frac{5}{6}+\frac{7}{12}-\frac{9}{20}+\frac{11}{30}-\frac{13}{42}=(1+\frac{1}{2})-(\frac{1}{2}+\frac{1}{3})+(\frac{1}{3}+\frac{1}{4})-(\frac{1}{4}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{6})-(\frac{1}{6}+\frac{1}{7})=1+\frac{1}{2}-\frac{1}{2}-\frac{1}{3}+\frac{1}{3}+\frac{1}{4}-\frac{1}{4}-\frac{1}{5}+\frac{1}{5}+\frac{1}{6}-\frac{1}{6}-\frac{1}{7}=1-\frac{1}{7}=\frac{6}{7}$.
②$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\cdots+\frac{1}{72}+\frac{1}{90}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\cdots+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}=1-\frac{1}{10}=\frac{9}{10}$.
(3)$\frac{5}{11}$ $\frac{3}{11}$ [解析]$\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+\frac{1}{63}+\frac{1}{99}=\frac{1}{2}×(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+\frac{1}{7}-\frac{1}{9}+\frac{1}{9}-\frac{1}{11})=\frac{1}{2}×(1-\frac{1}{11})=\frac{1}{2}×\frac{10}{11}=\frac{5}{11}$; $\frac{1}{3}-\frac{2}{15}+\frac{3}{35}-\frac{4}{63}+\frac{5}{99}=\frac{1}{4}×[(1+\frac{1}{3})-(\frac{1}{3}+\frac{1}{5})+(\frac{1}{5}+\frac{1}{7})-(\frac{1}{7}+\frac{1}{9})+(\frac{1}{9}+\frac{1}{11})]=\frac{1}{4}×(1+\frac{1}{11})=\frac{1}{4}×\frac{12}{11}=\frac{3}{11}$.
查看更多完整答案,请扫码查看


