《2025年实验班提优训练七年级数学上册人教版》

1. (2024·山东中考)下列有理数中,平方最大的数是(A)。
A.$3$
B.$\frac{1}{2}$
C.$-1$
D.$-2$

答案： A [解析]
∵$3^{2}=9$,$(\frac{1}{2})^{2}=\frac{1}{4}$,$(-1)^{2}=1$,$(-2)^{2}=4$,而$\frac{1}{4}＜1＜4＜9$,
∴选项中平方最大的数是3.故选A.

2. (2024·江西中考)计算：$(-1)^{2}= $1。

答案： 1 [解析]$(-1)^{2}=(-1)×(-1)=1$.

3. (教材P51例1·变式)老师出了一个计算题,计算：$(-3\frac{1}{2})^{3}$。立立的计算过程如下：
解：原式$=(-3)^{3}×(\frac{1}{2})^{3}$(第一步)
$=(-27)×\frac{1}{8}$(第二步)
$=-\frac{27}{8}$。(第三步)
(1)请问立立的计算过程是从第几步开始出错的？
(2)请把正确的计算过程写出来。

答案：
(1)从第一步开始出错.
(2)原式$=(-3-\frac{1}{2})^{3}=(-\frac{7}{2})^{3}=-\frac{7^{3}}{2^{3}}=-\frac{343}{8}$.

4. (2025·江苏南京鼓楼区期末)$-7^{2}$的值是(A)。
A.$-49$
B.$49$
C.$-14$
D.$14$

答案： A [解析]
∵$7^{2}=7×7=49$,
∴$-7^{2}=-49$.故选A.

5. (2025·浙江宁波海曙区期末)下列各数$4^{3}$,$(-\frac{1}{3})^{5}$,$-3^{2}$,$0$中,在数轴上所对应的点在原点右边的有(A)。
A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： A [解析]
∵$4^{3}=4×4×4=64＞0$,$(-\frac{1}{3})^{5}=-\frac{1}{243}＜0$,$-3^{2}=-9＞0$,$0=0$,
∴在数轴上所对应的点在原点右边的数是$4^{3}$,有1个.故选A.

6. (教材P52练习T2·变式)下列各数中,结果相等的是(B)。
A.$2^{3}和3^{2}$
B.$(-2)^{3}和-2^{3}$
C.$(-3)^{2}和-3^{2}$
D.$|-2|^{3}和(-2)^{3}$

答案： B [解析]A.
∵$2^{3}=8$,$3^{2}=9$,
∴$2^{3}≠3^{2}$.故此选项不符合题意;B.
∵$(-2)^{3}=-8$,$-2^{3}=-8$,
∴$(-2)^{3}=-2^{3}$.故此选项符合题意;C.
∵$(-3)^{2}=9$,$-3^{2}=-9$,
∴$(-3)^{2}≠-3^{2}$.故此选项不符合题意;D.
∵$|-2|^{3}=2^{3}=8$,$(-2)^{3}=-8$,
∴$|-2|^{3}≠(-2)^{3}$.故选B.

7. (2025·贵州贵阳期末)数轴上任意一点$A$,表示的数是$a$,下列各式一定成立的是(A)。

A.$a^{2}= (-a)^{2}$
B.$a^{3}= (-a)^{3}$
C.$-a^{2}= |-a^{2}|$
D.$a^{3}= |a^{3}|$

答案： A [解析]A.$a^{2}= (-a)^{2}$,故本选项符合题意;B.$a^{3}= (-a)^{3}$,故本选项不符合题意;C.$-a^{2}= |-a^{2}|$,故本选项不符合题意;D.$a^{3}= |a^{3}|$,故本选项不符合题意.故选A.

8. (跨学科 信息技术)(2025·湖南长沙期末)课本再现：进位制是人们为了计数和运算方便而约定的计数系统,约定逢十进一就是十进制,逢二进一就是二进制,也就是说逢几进一,就是几进制,几进制的基数就是几。规定当$a\neq0$时,$a^{0}= 1$。日常生活中,我们用十进制来表示数,表示十进制的数要用$10$个数码：$0$,$1$,$2$,$3$,$4$,$5$,$6$,$7$,$8$,$9$。例如：$168 = 1×10^{2}+6×10^{1}+8×10^{0}$。计算机中采用的是二进制,只要用到两个数码：$0$,$1$。如二进制中的$1010 = 1×2^{3}+0×2^{2}+1×2^{1}+0×2^{0}$,可以表示十进制中的$10$。
密码学是研究编制和破译密码的规律的一门学科,它与数学有密切关系。例如,有一种密钥破解方式,先将明码二进制数转成十进制数$x$后,再按以下规定获得密码：当$x$为奇数时,破解公式为$\frac{|3 - x|}{2}$,当$x$为偶数时,破解公式为$2x + 5$。按上述规定,则二进制明码“$101101$”译成密码为21。

答案： 21 [解析]$1×2^{5}+0×2^{4}+1×2^{3}+1×2^{2}+0×2^{1}+1×2^{0}=32+8+4+1=45$,则$\frac{|3-45|}{2}=21$,即二进制明码“101101”译成密码为21.

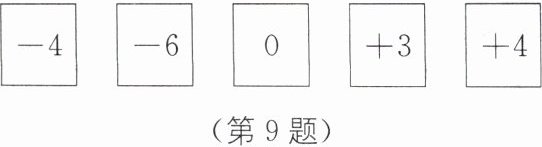
9. (2024·山东青岛期中)如图,小强有$5$张写着不同数字的卡片,请你按要求抽取卡片,完成下列各问题：
(1)从中取出$2$张卡片,使这$2$张卡片上数字乘积最大,如何抽取？最大值是多少？
(2)从中取出$2$张卡片,使这$2$张卡片上数字相除的商最小,如何抽取？最小值是多少？
(3)从中取出$2$张卡片,利用这$2$张卡片上数字进行某种运算,得到一个最大的数,如何抽取？最大的数是多少？
(4)从中取出$4$张卡片,用学过的运算方法,使结果为$24$,如何抽取？写出运算式子(一种即可)。

答案：
(1)抽取-4与-6,则其乘积最大为$-4×(-6)=24$.
(2)抽取-6与3,则其商最小为$-6÷3=-2$.
(3)抽取-6与4,则有最大的数为$(-6)^{4}=1296$.
(4)$(-6)×4×(-4+3)=24$(答案不唯一).