《2025年实验班提优训练七年级数学上册人教版》

1. 教材P53例3·变式 下列各组数中,其值相等的是(C).
A.$3^{2}和2^{3}$
B.$(-2)^{2}和-2^{2}$
C.$(-3)^{3}和-3^{3}$
D.$(-3×2)^{2}和-3×2^{2}$

答案： C 解析:A.$3^{2}=9,2^{3}=8,3^{2}≠2^{3}$,故A不符合题意;B.$(-2)^{2}=4,-2^{2}=-4,(-2)^{2}≠-2^{2}$,故B不符合题意;C.$(-3)^{3}=-27,-3^{3}=-27,(-3)^{3}=-3^{3}$,故C符合题意;D.$(-3×2)^{2}=(-6)^{2}=36,-3×2^{2}=-3×4=-12,$$(-3×2)^{2}≠-3×2^{2}$,故D不符合题意.故选C.

2. (2025·江苏南京鼓楼区期末)下列算式中,正确的是(C).
A.$(-32)÷4×(-8)= (-32)÷(-32)$
B.$\frac {1}{6}÷(\frac {1}{3}-\frac {1}{2})= \frac {1}{6}÷\frac {1}{3}-\frac {1}{6}÷\frac {1}{2}$
C.$(-2)^{3}×(-7)= 2^{3}×7$
D.$-(-0.2)^{4}= 0.2×0.2×0.2×0.2$

答案： C 解析:A.$(-32)÷4×(-8)=(-8)×(-8)$.故A不符合题意;B.$\frac {1}{6}÷(\frac {1}{3}-\frac {1}{2})=\frac {1}{6}÷(-\frac {1}{6})$,故B不符合题意;C.$(-2)^{3}×(-7)=2^{3}×7$.故C符合题意;D.$-(-0.2)^{4}=-0.2×0.2×0.2×0.2$,故D不符合题意.故选C.

3. 计算:$(-2)^{2}+(-2)×2=$0.

答案： 0 解析:$(-2)^{2}+(-2)×2=4+(-4)=0.$

4. (2024·广西中考)计算:$(-3)×4+(-2)^{2}.$

答案： 原式$=-12+4=-8.$

5. (2025·海南三亚期末)在计数制中,通常我们使用的是“十进位制”,即“逢十进一”,而计数制方法很多,如60进位制:60秒化为1分钟,60分钟化为1小时;24进位制:24小时化为一天;7进位制:7天化为1周…而二进位制是计算机处理数据的依据.已知二进位制与十进位制比较如下表:
|十进位制|0|1|2|3|4|5|6|…|
|二进位制|0|1|10|11|100|101|110|…|
将二进位制数10101010写成十进位制数为(B).
A.150
B.170
C.180
D.200

答案： B 解析:$10101010=1×2^{7}+0×2^{6}+1×2^{5}+0×2^{4}+1×$$2^{3}+0×2^{2}+1×2^{1}+0×2^{0}=128+32+8+2=170.$故选B.

6. 传统文化《周易》 (2025·安徽合肥瑶海区期末)《周易》历来被人们视作儒家群经之首,它表现了古代中华民族对万事万物深刻而又朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法,我们用近代术语解释为:把阳爻“——”当作数字“1”,把阴爻“——”当作数字“0”,则八卦所代表的数表示如下：

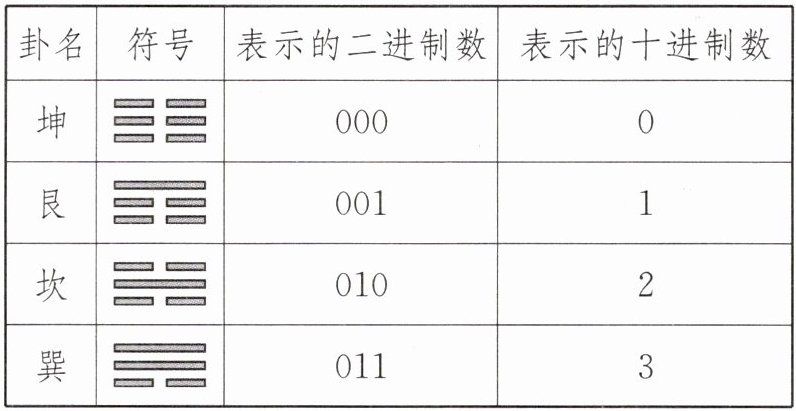
例如:“艮”卦所表示二进制数为001,转化为十进制数是$0×2^{2}+0×2^{1}+1×2^{0}= 1$,“巽”卦所表示二进制数为011,转化为十进制数是$0×2^{2}+1×2^{1}+1×2^{0}= 3$. (规定$a^{0}= 1,a≠0$)依次类推,则六十四卦中的“屯”卦,符号为“”,其表示的十进制数是(B).
A.33
B.34
C.35
D.36

答案： B

7. 中考新考法 新定义问题 (2025·福建福州期末)定义一种新运算“$\odot$”,规定运算法则为：$a\odot b= a^{b}+ab$(a,b均为整数,且$a≠0$),例如:$3\odot 2= 3^{2}+3×2= 15$,则$(-3)\odot 3$的值为-36.

答案： -36 解析:$\because a\odot b=a^{b}+ab$(a,b均为整数,且$a≠0),$$\therefore (-3)\odot 3=(-3)^{3}+(-3)×3=-27-9=-36.$

8. (2025·北京通州区期末)在$0\sim 40^{\circ }C$范围内,当温度每上升$1^{\circ }C$时,某种金属丝约伸长0.002mm;反之,当温度每下降$1^{\circ }C$时,金属丝约缩短0.002mm.把$20^{\circ }C的这种金属丝先加热到30^{\circ }C$,再使它冷却降温到$10^{\circ }C$.最后的长度比原长度约伸长____-0.02mm.

答案： -0.02 解析:$(10-20)×0.002=-10×0.002=-0.02$(mm),即最后的长度比原长度约伸长-0.02 mm.易错提示 本题考查有理数的混合运算,结合已知条件列得正确的算式是解题的关键.