第122页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
1.(2025·吉林大学尚德学校一模)等式的性质在生活中广泛应用.如图,a,b分别表示两位同学的身高,c表示台阶的高度,左边同学比右边同学高5厘米,图中两人的对话体现的数学原理可表示为(
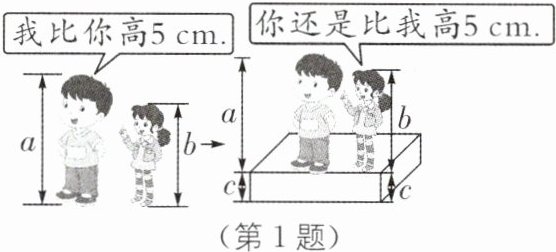
A.若$a = b + 5$,则$a + c = b + c + 5$
B.若$a = b + c$,则$a + 5 = b + c + 5$
C.若$a = b + 5$,则$ac = (b + 5)c$
D.若$a = b + 5$,则$\frac {a}{c} = \frac {b + 5}{c}$
A
).
A.若$a = b + 5$,则$a + c = b + c + 5$
B.若$a = b + c$,则$a + 5 = b + c + 5$
C.若$a = b + 5$,则$ac = (b + 5)c$
D.若$a = b + 5$,则$\frac {a}{c} = \frac {b + 5}{c}$
答案:
A 解析由图可知a=b+5,根据等式的性质1,将a=b+5的两边同时加c,得a+c=b+c+5,
∴A符合题意,B,C,D不符合题意.故选A.
解后反思 本题考查等式的性质,掌握等式的两个性质是解题的关键.
∴A符合题意,B,C,D不符合题意.故选A.
解后反思 本题考查等式的性质,掌握等式的两个性质是解题的关键.
2.一元一次方程$\frac {2x - 1}{3} - \frac {5x + 2}{6} = 1$,去分母、去括号后变形正确的是(
A.$4x - 2 - 5x + 2 = 1$
B.$4x - 2 - 5x - 2 = 1$
C.$4x - 2 - 5x + 2 = 6$
D.$4x - 2 - 5x - 2 = 6$
D
).A.$4x - 2 - 5x + 2 = 1$
B.$4x - 2 - 5x - 2 = 1$
C.$4x - 2 - 5x + 2 = 6$
D.$4x - 2 - 5x - 2 = 6$
答案:
D 解析$\frac{2x-1}{3}-\frac{5x+2}{6}=1$.
去分母,得2(2x-1)-(5x+2)=6.
去括号,得4x-2-5x-2=6.故选D.
去分母,得2(2x-1)-(5x+2)=6.
去括号,得4x-2-5x-2=6.故选D.
3.(2025·湖北武汉黄陂区期末)解方程:
(1)$3(x - 1) = 2(x + 4)$;
(2)$\frac {x + 1}{2} - 1 = \frac {2 - x}{4}$.
(1)$3(x - 1) = 2(x + 4)$;
(2)$\frac {x + 1}{2} - 1 = \frac {2 - x}{4}$.
答案:
(1)去括号,得3x-3=2x+8.
移项,得3x-2x=8+3.
合并同类项,得x=11.
(2)去分母,得2(x+1)-4=2-x.
去括号,得2x+2-4=2-x.
移项、合并同类项,得3x=4.
系数化为1,得$x=\frac{4}{3}$.
归纳总结 本题考查的是解一元一次方程,熟知去分母、去括号、移项、合并同类项、系数化为1是解一元一次方程的一般步骤是解题的关键.
(1)去括号,得3x-3=2x+8.
移项,得3x-2x=8+3.
合并同类项,得x=11.
(2)去分母,得2(x+1)-4=2-x.
去括号,得2x+2-4=2-x.
移项、合并同类项,得3x=4.
系数化为1,得$x=\frac{4}{3}$.
归纳总结 本题考查的是解一元一次方程,熟知去分母、去括号、移项、合并同类项、系数化为1是解一元一次方程的一般步骤是解题的关键.
(1)一商店以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,这两件衣服的进价分别是
(2)七年级实践小组调查,某款羽绒服以每件80元的价格购进了200件,并以每件120元的价格销售了一部分,为回笼资金,商场将剩下的羽绒服在原售价的基础上每件打6折销售,并全部销售完毕.已知这批羽绒服正好达到盈利35%的预期目标,请你算一算降价前共售出多少件?
设降价之前销售的数量为m件时,销售完这批羽绒服正好达到盈利35%的预期目标.
由题意,可得$120m+120×60\%×(200-m)-80×200=80×200×35\%$,解得m=150.
故降价之前销售的羽绒服数量为150件时,销售完这批羽绒服正好达到盈利35%的预期目标.
48
元和80
元,卖这两件衣服总的来说是亏损
(填“盈利”“亏损”或“不盈不亏”).(2)七年级实践小组调查,某款羽绒服以每件80元的价格购进了200件,并以每件120元的价格销售了一部分,为回笼资金,商场将剩下的羽绒服在原售价的基础上每件打6折销售,并全部销售完毕.已知这批羽绒服正好达到盈利35%的预期目标,请你算一算降价前共售出多少件?
设降价之前销售的数量为m件时,销售完这批羽绒服正好达到盈利35%的预期目标.
由题意,可得$120m+120×60\%×(200-m)-80×200=80×200×35\%$,解得m=150.
故降价之前销售的羽绒服数量为150件时,销售完这批羽绒服正好达到盈利35%的预期目标.
答案:
(1)48 80 亏损
(2)设降价之前销售的数量为m件时,销售完这批羽绒服正好达到盈利35%的预期目标.
由题意,可得$120m+120×60\%×(200-m)-80×200=80×200×35\%$,解得m=150.
故降价之前销售的羽绒服数量为150件时,销售完这批羽绒服正好达到盈利35%的预期目标.
(1)48 80 亏损
(2)设降价之前销售的数量为m件时,销售完这批羽绒服正好达到盈利35%的预期目标.
由题意,可得$120m+120×60\%×(200-m)-80×200=80×200×35\%$,解得m=150.
故降价之前销售的羽绒服数量为150件时,销售完这批羽绒服正好达到盈利35%的预期目标.
5.周末小明和爸爸来到了一处农场,并体验了农场的骑马项目,马场有一个如图所示的长为600m的环形跑道,若把跑道从A,B,C,D处分成长度相等的四段,小明和爸爸在骑师的引导下分别从A,D两处同时出发,沿箭头方向相向而行,小明骑小马和爸爸骑大马的平均速度分别为5m/s、7m/s.
(1)多久后两人首次相遇? 并说出此时他们在跑道上的具体位置.
(2)在首次相遇后第二次相遇前,又经过多长时间两人相距60m?
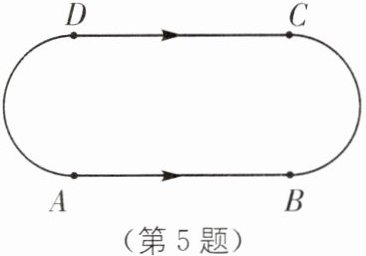
(1)多久后两人首次相遇? 并说出此时他们在跑道上的具体位置.
(2)在首次相遇后第二次相遇前,又经过多长时间两人相距60m?

答案:
(1)设x秒后两人首次相遇.
依题意,得到方程$5x+7x=600×\frac{3}{4}$,解得x=37.5.
小明的路程=$5×37.5=187.5$(米),
$187.5-600×\frac{1}{4}=37.5$(米).
故37.5秒后两人首次相遇,此时他们在弯道BC上,且离点B 37.5米的位置.
(2)设又经过y秒后两人背靠背或面对面相距60 m.
依题意,得5y+7y=60或5y+7y=600-60,
解得y=5或y=45.
故在首次相遇后第二次相遇前,又经过5秒或45秒时,两人相距60 m.
思路引导 本题考查了一元一次方程的应用,解题的关键是看清是相遇问题以及找到两人相距60 m时所走的路程.
(1)设x秒后两人首次相遇.
依题意,得到方程$5x+7x=600×\frac{3}{4}$,解得x=37.5.
小明的路程=$5×37.5=187.5$(米),
$187.5-600×\frac{1}{4}=37.5$(米).
故37.5秒后两人首次相遇,此时他们在弯道BC上,且离点B 37.5米的位置.
(2)设又经过y秒后两人背靠背或面对面相距60 m.
依题意,得5y+7y=60或5y+7y=600-60,
解得y=5或y=45.
故在首次相遇后第二次相遇前,又经过5秒或45秒时,两人相距60 m.
思路引导 本题考查了一元一次方程的应用,解题的关键是看清是相遇问题以及找到两人相距60 m时所走的路程.
查看更多完整答案,请扫码查看


