《2025年名校题库九年级数学全一册北师大版》

1. (天府新区一诊)如图,直线 AB 与反比例函数$y= \frac {k}{x}$的图象交于 A,B 两点,与 x 轴交于点 M 且满足$\frac {MA}{MB}= 2$,连接 AO 并延长交反比例函数图象于点 C,连接 BC. 若$\triangle ABC$的面积为 24,则 k 的值为____.

答案：
16 【解析】如图,分别过 A,B 两点作 x 轴的垂线,垂足分别为 E,F,则$\triangle AEM\backsim \triangle BFM.\because \frac {MA}{MB}=2,\therefore \frac {AE}{BF}=\frac {MA}{MB}=2$,即$AE=2BF$.设点 B 的坐标为$(\frac {k}{m},m)$,则点 A 的坐标为$(-\frac {k}{2m},-2m).\because A$,C 两点关于原点对称,
∴点 C 的坐标为$(\frac {k}{2m},2m)$.连接 OB,$\because \triangle ABC$的面积为 24,$\therefore \triangle BCO$的面积为 12. 过点 C 作 x 轴的垂线,垂足为 P,由$S_{\triangle COP}+S_{梯形CBFP}=S_{\triangle BCO}+S_{\triangle BOF}$,且$S_{\triangle COP}=S_{\triangle BOF}$,得$S_{梯形CBFP}=S_{\triangle BCO}=12,\therefore \frac {(m+2m)(\frac {k}{m}-\frac {k}{2m})}{2}=12$,解得$k=16$.

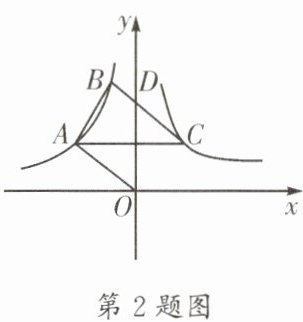
2. (双流区一诊)已知双曲线$y= -\frac {10}{x}(x＜0)和y= \frac {k}{x}(x＞0)$的图象如图所示,直线 OA 与双曲线$y= -\frac {10}{x}$交于点 A,将直线 OA 向上平移与双曲线$y= -\frac {10}{x}$交于点 B,与 y 轴交于点 D,与双曲线$y= \frac {k}{x}$交于点 C,$S_{\triangle ABC}= 12,BD= \frac {1}{2}CD$,则$k= $____.

答案：
8 【解析】如图,连接 OB,OC,过点 B 作$BE⊥y$轴于点 E,过点 C 作$CF⊥y$轴于点 F.$\because OA// BC,\therefore S_{\triangle OBC}=S_{\triangle ABC}=12.\because BD=\frac {1}{2}CD,\therefore S_{\triangle ODB}=4,S_{\triangle ODC}=8.\because S_{\triangle OBE}=\frac {1}{2}×|-10|=5,\therefore S_{\triangle DBE}=5-4=1.\because \triangle BED\backsim \triangle CFD,\therefore \frac {S_{\triangle CFD}}{S_{\triangle BED}}=(\frac {DC}{BD})^{2}=4,\therefore S_{\triangle CFD}=1×4=4,\therefore S_{\triangle OCF}=S_{\triangle ODC}-S_{\triangle CFD}=8-4=4,\therefore k=8$.

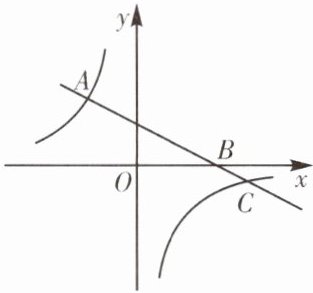
3. (金牛区期末)如图,在平面直角坐标系中,一次函数$y= ax+3(a≠0)$的图象与x 轴交于点 B(6,0),与反比例函数$y= \frac {k}{x}(k≠0)$的图象交于 A,C 两点,已知点 A 的纵坐标为 4.
(1)求一次函数和反比例函数的解析式;
(2)若点 P 在 x 轴上,当$\triangle PAC$的面积为 10 时,求点 P 的坐标.

答案：
解:
(1)$\because$点$B(6,0)$在直线$y=ax+3$上,$\therefore 6a+3=0$,解得$a=-\frac {1}{2}$,$\therefore$一次函数的解析式为$y=-\frac {1}{2}x+3$.$\because$点 A 在直线$y=-\frac {1}{2}x+3$上,且点 A 的纵坐标为 4,$\therefore -\frac {1}{2}x+3=4$,解得$x=-2$,$\therefore$点 A 的坐标为$(-2,4)$.$\because$反比例函数$y=\frac {k}{x}$的图象经过点 A,$\therefore k=-2×4=-8$,$\therefore$反比例函数的解析式为$y=-\frac {8}{x}$.
(2)联立方程组$\left\{\begin{array}{l} y=-\frac {1}{2}x+3,\\ y=-\frac {8}{x},\end{array}\right. $解得$\left\{\begin{array}{l} x=8,\\ y=-1\end{array}\right. $或$\left\{\begin{array}{l} x=-2,\\ y=4,\end{array}\right. $$\therefore$点 C 的坐标为$(8,-1)$.如图,连接 AP,PC.$\because S_{\triangle PAC}=S_{\triangle PAB}+S_{\triangle PBC}=\frac {1}{2}×PB×4+\frac {1}{2}×PB×1=10$,解得$PB=4$.又$\because B(6,0)$,$\therefore$点 P 的坐标为$(2,0)$或$(10,0)$.