《2025年名校题库九年级数学全一册北师大版》

$6. ($天府新区一诊$)$已知点$A(x_1,y_1),B(x_2,y_2)$在反比例函数$y= \frac {3-2m}{x}$的图象上$,$当$x_1＜x_2＜0$时$,y_1＞y_2,$则$m$的取值范围为$(D)$
A. m＞$\frac {2}{3}$
B. m＜$\frac {2}{3}$
C. m＞$\frac {3}{2}$
D. m＜$\frac {3}{2}$

答案： D

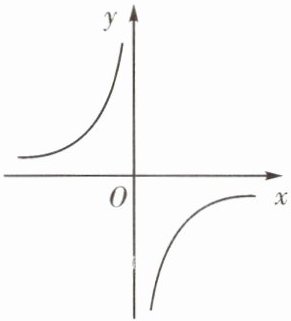
7. (锦江区二诊)已知函数$y= \frac {m-1}{x}(m≠0)$的图象如图所示,有以下结论：①m＜1；②在每个分支上,y随x的增大而增大；③若点A(-2,a)和点B(4,b)在该函数的图象上,则a＜b；④若点P(x,y)在该函数的图象上,则点P(-x,-y)也在该函数的图象上。下列选项正确的是(B)

A. ①②③
B. ①②④
C. ①③④
D. ①②③④

答案： B

8. (龙泉驿区一诊)若反比例函数$y= \frac {m+1}{x}$的图象在第一、三象限,则m的取值范围是$ m ＞ -1 $。

答案： $ m ＞ -1 $

9. (天府新区一诊)在反比例函数$y= \frac {k-3}{x}$图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是$ k ＞ 3 $。

答案： $ k ＞ 3 $

10. (高新区一诊)关于反比例函数$y= -\frac {2}{x}$的图象,当y＞1时,x的取值范围是$-2 ＜ x ＜ 0$。

答案： $ -2 ＜ x ＜ 0 $

11. (石室联中)若点A(m,-3)在反比例函数$y= \frac {6}{x}$的图象上,则当函数值y≥-2时,自变量x的取值范围是$ x \leq -3 $ 或 $ x ＞ 0 $。

答案： $ x \leq -3 $ 或 $ x ＞ 0 $

12. (金牛区一诊)若点A(1,y_1),B(2,y_2),C(-3,y_3)在双曲线$y= \frac {a^{2}+1}{x}$上,则y_1,y_2,y_3的大小关系是$ y_1 ＞ y_2 ＞ y_3 $。

答案： $ y_1 ＞ y_2 ＞ y_3 $

13. (双流区一诊)若点A(m+2,y₁),B(m-2,y₂)在反比例函数$y= \frac {k}{x}(k＜0)$的图象上,且m+2＞m-2,y₁＜y₂,则m的取值范围是______$-2＜m＜2$。

答案： $ -2 ＜ m ＜ 2 $ 【解析】
∵ 反比例函数 $ y = \frac{k}{x} $ ($ k ＜ 0 $)，
∴ 其图象位于第二、四象限，在每个象限内 $ y $ 随 $ x $ 的增大而增大.
∵ 点 $ A(m + 2, y_1) $，$ B(m - 2, y_2) $ 在反比例函数 $ y = \frac{k}{x} $ ($ k ＜ 0 $) 的图象上，且 $ m + 2 ＞ m - 2 $，$ y_1 ＜ y_2 $，
∴ 点 $ A(m + 2, y_1) $ 和点 $ B(m - 2, y_2) $ 不在同一象限，则点 $ A(m + 2, y_1) $ 在第四象限，点 $ B(m - 2, y_2) $ 在第二象限，
∴ $ \begin{cases} m + 2 ＞ 0, \\ m - 2 ＜ 0, \end{cases} $ 解得 $ -2 ＜ m ＜ 2 $.