《2025年名校题库九年级数学全一册北师大版》

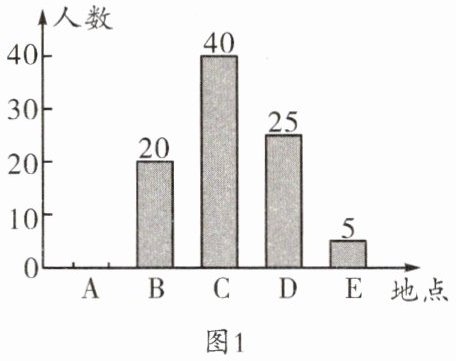
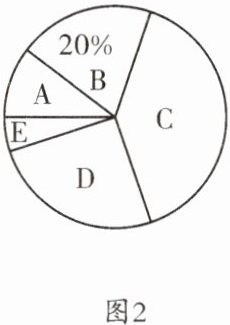
18. (青羊区一诊)某中学计划组织学生外出开展研学活动,在选择研学活动地点时,随机抽取了部分学生进行调查,要求被调查的学生从 $ A $,$ B $,$ C $,$ D $,$ E $ 五个研学活动地点中选择自己最喜欢的一个,根据调查结果,编制了如下两幅不完整的统计图。根据统计图提供的信息,解答下列问题：
(1)在这次调查中,一共抽取了______名学生。
(2)请把图 $ 1 $ 中缺失的数据补充完整；图 $ 2 $ 中研学活动地点 $ C $ 所在扇形的圆心角的度数是______。
(3)在选择 $ E $ 地的 $ 5 $ 人中,有 $ 2 $ 人来自九年级(1)班,$ 3 $ 人来自九年级(2)班,现在要从这 $ 5 $ 人中任选两人做研学规划分享,求选中的两人恰好来自同一个班的概率。

答案：
解:
(1)100
(2)选择A地的人数为100−20−40−25 - 5 = 10(人).
　补全图形如下:
　　　　
　图2中研学活动地点C所在扇形的圆心角的度数:144°
(3)将来自九年级
(1)班的两人分别记为a,b,来自九年级
(2)班的3人分别记为c,d,e,列表如下:
　　　　　　a　　　　b　　　c　　　d　　　e
　　　a　　　　　　　(a,b)　(a,c) (a,d) (a,e)
　　　b　　　(b,a) (b,c)　　(b,d) (b,e)
　　　c　　　(c,a)　　(c,b) (c,d) (c,e)
　　　d　　(d,a) (d,b) (d,c) (d,e)
　　　e　　　(e,a) (e,b) (e,c) (e,d)
　共有20种等可能的结果，其中选中的两人恰好来自同一个班的结果有:(a,b),(b,a),(c,d)，(c,e),(d,c),(d,e),(e,c),(e,d),共8种,
　
∴选中的两人恰好来自同一个班的概率为$\frac{8}{20}$=$\frac{2}{5}$.

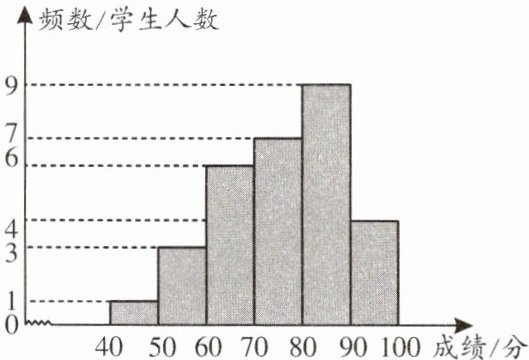
19. (西川)为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择：$ A $. 趣味数学；$ B $. 博乐阅读；$ C $. 快乐英语；$ D $. 硬笔书法。某年级共有 $ 100 $ 名学生选择了 $ A $ 课程,为了解本年级选择 $ A $ 课程学生的学习情况,从这 $ 100 $ 名学生中随机抽取了 $ 30 $ 名学生进行测试,将他们的成绩(百分制)分成六组,绘制成如图所示的频数分布直方图。
(1)已知 $ 70 \leq x ＜ 80 $ 这组的数据为 $ 72 $,$ 73 $,$ 74 $,$ 75 $,$ 76 $,$ 76 $,$ 79 $,则这组数据的中位数是______,众数是______；
(2)根据题中信息,估计该年级选择 $ A $ 课程学生成绩在 $ 80 \leq x ＜ 90 $ 的总人数；
(3)该年级学生小乔随机选择了一门课程,则小乔选中课程 $ D $ 的概率是______；
(4)该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程 $ C $,那么他俩第二次同时选择课程 $ A $ 或课程 $ B $ 的概率是多少？请用列表法或画树状图的方法加以说明。

答案：
解:
(1)75　76
(2)观察频数分布直方图可知，抽取的30名学生成绩在80≤x＜90范围内的有9人，占比为$\frac{9}{30}$，那么估计该年级100名学生成绩在80≤x＜90范围内，选取A课程的总人数为100×$\frac{9}{30}$ = 30(人).
(3)$\frac{1}{4}$
(4)因为该年级每名学生选两门不同的课程，小张和小王第一次都选了课程C，画树状图如下:
　　
由图可知，等可能的结果共有9种，他俩第二次同时选择课程A或课程B的情况有2种，所以他俩第二次同时选择课程A或课程B的概率是$\frac{2}{9}$.