《2025年名校题库九年级数学全一册北师大版》

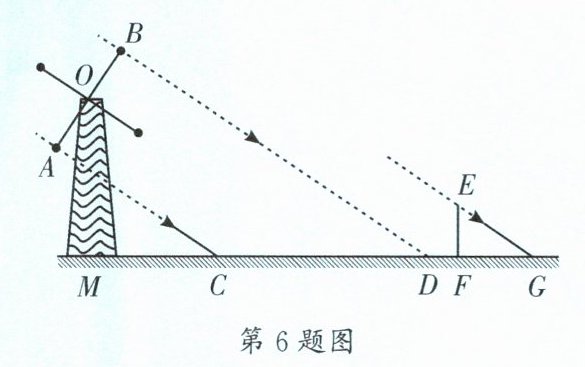
6. (成华区一诊)如图是某风车的示意图,其大小相同的四个叶片均匀分布,点M在旋转中心O的正下方。某一时刻,太阳光恰好垂直照射叶片OA,OB,叶片的影子为线段CD,测得MC= 8.5米,CD= 13米,此时垂直于地面的标杆EF与它的影子FG的比为2:3(其中点M,C,D,F,G在水平地面上),则OM的高度为______米,叶片OA的长为______米.

答案：
10　$\sqrt{13}$　[解析]如图，过点O作OP//BD,交MG于点P,过点P作PN⊥BD于点N，则OB=PN.
　　
∵AC//BD,
∴AC//OP//BD,
∴$\frac{OA}{OB}$=$\frac{CP}{PD}$,∠EGF=∠OPM.
∵OA=OB,
∴CP=PD=$\frac{1}{2}$CD=6.5(米)，
∴MP=CM+CP=8.5+6.5=15(米).
∵△EGF∽△OPM,
∴$\frac{EF}{FG}$=$\frac{OM}{MP}$=$\frac{2}{3}$,
∴$\frac{EF}{EG}$=$\frac{2}{\sqrt{13}}$,
∴OM=$\frac{2}{3}$×15=10(米).
∵DB//EG,
∴∠EGF=∠NDP.又
∵∠PND=∠EFG=90°,
∴△EFG∽△PND,
∴$\frac{EF}{EG}$=$\frac{PN}{PD}$,
∴$\frac{2}{\sqrt{13}}$=$\frac{PN}{6.5}$,
∴OB=PN=$\sqrt{13}$米，
∴OA=OB=$\sqrt{13}$米.

7. (青羊区一诊)周末小明与父亲爬山,在停车场附近看到了一棵银杏树AB,AB垂直于地面,满树金灿灿的叶子非常好看,小明想测量这棵树的高度,他发现阳光下树的影子恰好落在地面和一斜坡上(如图所示),此时测得地面上的影长BC为8m,坡面上的影长CD为4m,斜坡与水平地面所成的锐角为30°,同一时刻,一根长为1m垂直于地面放置的标杆在地面上的影长为2m.(参考数据：$\sqrt{3}\approx1.732$)
(1)求点D到水平地面的距离；
(2)求树的高度(结果精确到0.1m).

答案：
解:
(1)如图，延长AD,BC交于点E,过点D作DH⊥BC于点H.
　在Rt△CDH中,∠CHD=90°,∠DCH=30°,CD=4m,
∴DH=$\frac{1}{2}$CD=2m.
　故点D到水平地面的距离为2m.
(2)CH=$\sqrt{CD^{2}-DH^{2}}$=$\sqrt{4^{2}-2^{2}}$=2√3(m),
∵同一时刻，一根长为1m垂直于地面放置的标杆在地面上的影长为2m,
∴HE=2DH=4m,
∴BE=BC+CH+HE=8+2$\sqrt{3}$+4=(12+2$\sqrt{3}$)m,
∴AB=BE÷2=6+$\sqrt{3}$≈7.7(m).
　故这棵树的高度约为7.7m.
　　　　　

8. (锦江区一诊)如图,三根木杆AB,CD,EF竖直立于地平面,点B,D,F在同一条直线上,且每两根木杆之间的距离为6米,即BD= DF= 6米,木杆AB,CD的影子分别为BG,DH.
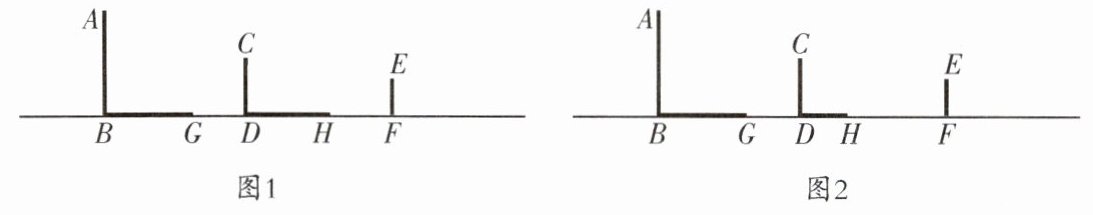
(1)在图1、图2两个示意图中,反映阳光下情形的是图______,反映灯光下情形的是图______；(填图形序号)
(2)请在图1中画出表示木杆EF的影长的线段；
(3)已知木杆AB长为3.6米,木杆CD长为2.25米,木杆EF长为1.5米,在图1中测得木杆AB,CD的影长BG= DH= 4米,求木杆EF的影长.

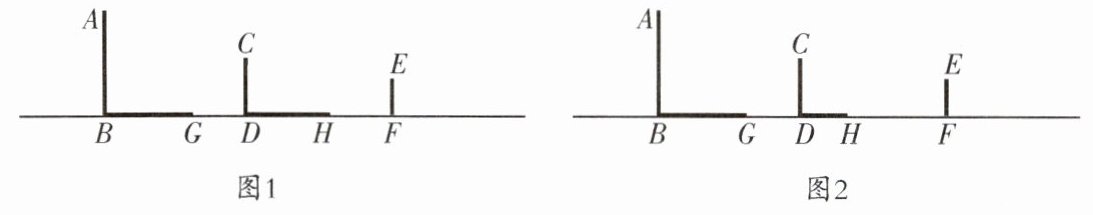
答案：
解:
(1)2　1
(2)如图，线段FM即为所求.
　　
(3)如图，过点O作OR垂直于地平面，垂足为R，设BR=x米,OR=y米.
∵AB⊥BG,OR⊥BG,
∴△ABG∽△ORG,
∴$\frac{AB}{OR}$=$\frac{GB}{GR}$,$\frac{3.6}{y}$=$\frac{4}{4+x}$ ①.
　同法可得$\frac{CD}{OR}$=$\frac{DH}{RH}$,$\frac{2.25}{y}$=$\frac{4}{4+6+x}$ ②.
　由①②解得$\begin{cases}x = 6, \\ y = 9, \end{cases}$经检验,$\begin{cases}x = 6, \\ y = 9 \end{cases}$是分式方程组的解，且符合题意.
　同法可得$\frac{EF}{OR}$=$\frac{FM}{RM}$,$\frac{1.5}{9}$=$\frac{FM}{FM+18}$,解得FM=3.6,经检验,FM=3.6是分式方程的解，且符合题意.
∴木杆EF的影长为3.6米.