第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
6. (天府新区二诊)在$Rt△ABC$中,$BC= 2,∠C= 90^{\circ },∠A= 30^{\circ }$,点 E 在线段 AC 上,点 F 在线段 AB 上,将$∠A$沿 EF 翻折使顶点 A 落在直线 BC 上的点 D 处.
(1)当$DF// AC$时,求 AF 的长;
(2)当 B,C,D 中一点为另两点组成的线段的中点时,求 AF 的长;
(3)如图 2,BG 平分$∠ABC$交 ED 于点 G,当点 D 在线段 BC 上时,求 GD 的最小值.
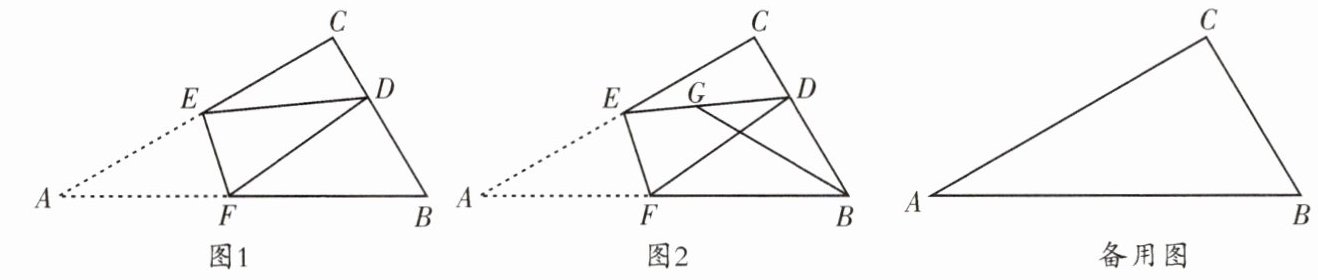
(1)当$DF// AC$时,求 AF 的长;
(2)当 B,C,D 中一点为另两点组成的线段的中点时,求 AF 的长;
(3)如图 2,BG 平分$∠ABC$交 ED 于点 G,当点 D 在线段 BC 上时,求 GD 的最小值.

答案:
解:
(1) $\because \angle C = 90^{\circ},\angle A = 30^{\circ},BC = 2,\therefore AB = 2BC = 4,\angle B = 60^{\circ},\therefore AC = \sqrt{AB^{2}-BC^{2}} = 2\sqrt{3}$. $\because DF// AC,\therefore \angle A = \angle DFB = 30^{\circ}$, $\therefore \angle FDB = 90^{\circ}$. $\because \angle A = \angle EDF = 30^{\circ},\therefore \angle CDE = \angle B = 60^{\circ}$, $\therefore DE// AB,\therefore$ 四边形 $AEDF$ 是平行四边形, $\angle CED = 30^{\circ}$. 又 $\because AE = ED,\therefore$ 四边形 $AEDF$ 是菱形, $\therefore AF = AE$. $\because \angle C = 90^{\circ},\angle CED = 30^{\circ},\therefore DE = 2CD,EC = \sqrt{3}CD,\therefore AE = DE = 2CD,\therefore AC = AE + EC = 2CD + \sqrt{3}CD = 2\sqrt{3},\therefore CD = 4\sqrt{3}-6$, $\therefore AF = AE = 2CD = 8\sqrt{3}-12$.
(2) 如图 1, 当 $CD = DB$ 时, 过点 $D$ 作 $DT\perp AB$ 于点 $T$. $\because$ 在 $Rt\triangle DBT$ 中, $BD = 1,\angle BDT = 30^{\circ}$, $\therefore BT = \frac{1}{2},\therefore DT = \sqrt{BD^{2}-BT^{2}} = \frac{\sqrt{3}}{2},AT = AB - BT = \frac{7}{2}$. 设 $AF = FD = x$, 则 $FT = \frac{7}{2}-x$. 在 $Rt\triangle FDT$ 中, 有 $x^{2} = (\frac{7}{2}-x)^{2}+(\frac{\sqrt{3}}{2})^{2}$, 解得 $x = \frac{13}{7},\therefore AF = \frac{13}{7}$.
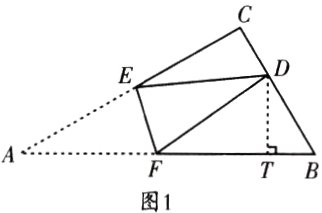
如图 2, 当 $CD = CB = 2$ 时, 过点 $D$ 作 $DL\perp AB$ 于点 $L$. $\because$ 在 $Rt\triangle BDL$ 中, $\angle D = 30^{\circ},BD = 4$, $\therefore BL = \frac{1}{2}BD = 2,\therefore DL = \sqrt{BD^{2}-BL^{2}} = 2\sqrt{3},AL = AB - BL = 2$. 设 $AF = DF = y$, 则 $FL = y - 2$. 在 $Rt\triangle DLF$ 中, $DF^{2} = FL^{2}+DL^{2}$, 即 $y^{2} = (y - 2)^{2}+(2\sqrt{3})^{2}$, 解得 $y = 4,\therefore AF = 4$, 此时点 $B$ 与点 $F$ 重合. 综上所述, $AF$ 的长为 $\frac{13}{7}$ 或 $4$.
(3) 如图 3, 连接 $FG$.
$\because BG$ 平分 $\angle ABC,\therefore \angle FBG = \angle DBG = 30^{\circ}$. $\because \angle EDF = \angle A = 30^{\circ},\therefore \angle FDG = \angle FBG$, $\therefore \angle GFD = \angle GBD = 30^{\circ}$, $\therefore \angle GFD = \angle GDF = 30^{\circ}$, $\therefore DG = FG$, 易得 $DF = \sqrt{3}DG$, $\therefore$ 当 $DF$ 最小时, $DG$ 的值最小. 过点 $D$ 作 $DH\perp AB$ 于点 $H$. 设 $AF = DF = a,DB = b$, 则 $BH = \frac{1}{2}BD = \frac{1}{2}b,DH = \frac{\sqrt{3}}{2}b$. $\because$ 在 $Rt\triangle DFH$ 中, $DF^{2} = DH^{2}+FH^{2},\therefore a^{2} = (\frac{\sqrt{3}}{2}b)^{2}+(4 - a - \frac{1}{2}b)^{2}$, 整理, 得 $a = \frac{b^{2}-4b + 16}{8 - b} = -12 + (8 - b) + \frac{48}{8 - b},\therefore a\geq -12 + 2\sqrt{48} = 8\sqrt{3}-12$, 即 $DF$ 的最小值为 $8\sqrt{3}-12$, $\therefore DG$ 的最小值为 $\frac{DF}{\sqrt{3}} = 8 - 4\sqrt{3}$.

解:
(1) $\because \angle C = 90^{\circ},\angle A = 30^{\circ},BC = 2,\therefore AB = 2BC = 4,\angle B = 60^{\circ},\therefore AC = \sqrt{AB^{2}-BC^{2}} = 2\sqrt{3}$. $\because DF// AC,\therefore \angle A = \angle DFB = 30^{\circ}$, $\therefore \angle FDB = 90^{\circ}$. $\because \angle A = \angle EDF = 30^{\circ},\therefore \angle CDE = \angle B = 60^{\circ}$, $\therefore DE// AB,\therefore$ 四边形 $AEDF$ 是平行四边形, $\angle CED = 30^{\circ}$. 又 $\because AE = ED,\therefore$ 四边形 $AEDF$ 是菱形, $\therefore AF = AE$. $\because \angle C = 90^{\circ},\angle CED = 30^{\circ},\therefore DE = 2CD,EC = \sqrt{3}CD,\therefore AE = DE = 2CD,\therefore AC = AE + EC = 2CD + \sqrt{3}CD = 2\sqrt{3},\therefore CD = 4\sqrt{3}-6$, $\therefore AF = AE = 2CD = 8\sqrt{3}-12$.
(2) 如图 1, 当 $CD = DB$ 时, 过点 $D$ 作 $DT\perp AB$ 于点 $T$. $\because$ 在 $Rt\triangle DBT$ 中, $BD = 1,\angle BDT = 30^{\circ}$, $\therefore BT = \frac{1}{2},\therefore DT = \sqrt{BD^{2}-BT^{2}} = \frac{\sqrt{3}}{2},AT = AB - BT = \frac{7}{2}$. 设 $AF = FD = x$, 则 $FT = \frac{7}{2}-x$. 在 $Rt\triangle FDT$ 中, 有 $x^{2} = (\frac{7}{2}-x)^{2}+(\frac{\sqrt{3}}{2})^{2}$, 解得 $x = \frac{13}{7},\therefore AF = \frac{13}{7}$.

如图 2, 当 $CD = CB = 2$ 时, 过点 $D$ 作 $DL\perp AB$ 于点 $L$. $\because$ 在 $Rt\triangle BDL$ 中, $\angle D = 30^{\circ},BD = 4$, $\therefore BL = \frac{1}{2}BD = 2,\therefore DL = \sqrt{BD^{2}-BL^{2}} = 2\sqrt{3},AL = AB - BL = 2$. 设 $AF = DF = y$, 则 $FL = y - 2$. 在 $Rt\triangle DLF$ 中, $DF^{2} = FL^{2}+DL^{2}$, 即 $y^{2} = (y - 2)^{2}+(2\sqrt{3})^{2}$, 解得 $y = 4,\therefore AF = 4$, 此时点 $B$ 与点 $F$ 重合. 综上所述, $AF$ 的长为 $\frac{13}{7}$ 或 $4$.
(3) 如图 3, 连接 $FG$.
$\because BG$ 平分 $\angle ABC,\therefore \angle FBG = \angle DBG = 30^{\circ}$. $\because \angle EDF = \angle A = 30^{\circ},\therefore \angle FDG = \angle FBG$, $\therefore \angle GFD = \angle GBD = 30^{\circ}$, $\therefore \angle GFD = \angle GDF = 30^{\circ}$, $\therefore DG = FG$, 易得 $DF = \sqrt{3}DG$, $\therefore$ 当 $DF$ 最小时, $DG$ 的值最小. 过点 $D$ 作 $DH\perp AB$ 于点 $H$. 设 $AF = DF = a,DB = b$, 则 $BH = \frac{1}{2}BD = \frac{1}{2}b,DH = \frac{\sqrt{3}}{2}b$. $\because$ 在 $Rt\triangle DFH$ 中, $DF^{2} = DH^{2}+FH^{2},\therefore a^{2} = (\frac{\sqrt{3}}{2}b)^{2}+(4 - a - \frac{1}{2}b)^{2}$, 整理, 得 $a = \frac{b^{2}-4b + 16}{8 - b} = -12 + (8 - b) + \frac{48}{8 - b},\therefore a\geq -12 + 2\sqrt{48} = 8\sqrt{3}-12$, 即 $DF$ 的最小值为 $8\sqrt{3}-12$, $\therefore DG$ 的最小值为 $\frac{DF}{\sqrt{3}} = 8 - 4\sqrt{3}$.

查看更多完整答案,请扫码查看


