《2025年名校题库九年级数学全一册北师大版》

8. (高新区期末)
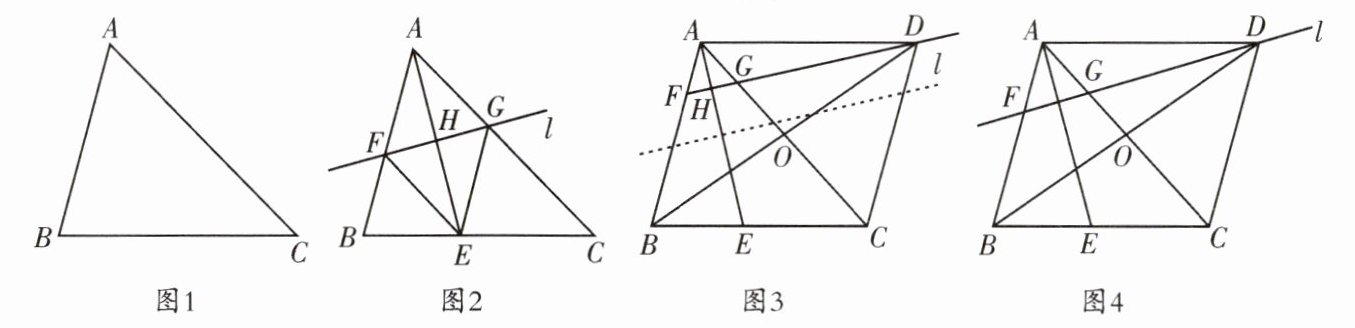
(1)【数学初探】在数学课上,叶老师提出了一个探究型问题:“如图 1,你能借助锐角△ABC 画出一个菱形,使∠A 为该菱形的一个内角吗?”雷同学提出了自己的见解:如图 2,①作∠BAC 的平分线 AE,交 BC 于点 E;②作 AE 的中垂线 l 分别交 AB,AC,AE 于点 F,G,H;③连接 EF,EG,则四边形 AFEG 是菱形. 请你帮助雷同学证明四边形 AFEG 是菱形.
(2)【深入探究】雷同学开启大胆尝试,如图 3,将△ABC 的中线 BO 延长至点 D,使 DO= OB,连接 AD,CD,平移图 2 中的直线 l(平移过程中直线 l 与 AB,AC,AE 的交点仍为 F,G,H),当直线 l 恰好经过点 D 时,他通过测量发现了线段 OG 与线段 BF 存在特定的数量关系. 请你写出线段 OG 与线段 BF 的数量关系,并求证.
(3)【迁移应用】如图 4,在(2)的条件下,若∠BAC= 60°,且 $\frac{S_{△DOG}}{S_{△DBF}}= \frac{3}{8}$ 时,求 $\frac{AD}{AB}$ 的值.

答案：

(1) 证明: $ \because AE $ 平分 $ \angle BAC $, $ \therefore \angle BAE = \angle CAE $.
$ \because FG $ 垂直平分 $ AE $, $ \therefore \angle AHF = \angle AHG = 90^{\circ} $, $ AH = EH $.
在 $ \triangle AHF $ 和 $ \triangle AHG $ 中, $ \left\{ \begin{array} { l } { \angle F A H = \angle G A H }, \\ { A H = A H }, \\ { \angle A H F = \angle A H G }, \end{array} \right. $
$ \therefore \triangle A H F \cong \triangle A H G ( A S A ) $,
$ \therefore H F = H G $, $ \therefore AE $ 与 $ FG $ 互相垂直平分, $ \therefore $ 四边形 $ AFEG $ 是菱形.
(2) 解: $ B F = 2 O G $.
证明: 如图 1, 取 $ DF $ 的中点 $ K $, 连接 $ OK $.
$ \because O B = O D $, $ \therefore O $ 是 $ BD $ 的中点, $ \therefore OK $ 是 $ \triangle BDF $ 的中位线,
$ \therefore B F = 2 O K $, $ O K // A B $, $ \therefore \angle O K G = \angle A F G $.
$ \because $ 平移题图 2 中的直线 $ l $ 恰好经过点 $ D $,
$ \therefore D F \perp A E $.
由
(1)可知, $ \triangle A H F \cong \triangle A H G $, $ \therefore \angle A F G = \angle A G F $.
$ \because \angle A G F = \angle O G K $, $ \therefore \angle O G K = \angle O K G $,
$ \therefore O K = O G $, $ \therefore B F = 2 O G $.


(3) 解: 如图 2, 取 $ DF $ 的中点 $ K $, 连接 $ OK $, 过点 $ D $ 作 $ D T \perp A B $ 交 $ B A $ 的延长线于点 $ T $, 过点 $ B $ 作 $ B R \perp D F $ 于点 $ R $, 过点 $ O $ 作 $ O Q \perp D F $ 于点 $ Q $.
由
(1)
(2)知, $ A F = A G $, $ O K = O G $, $ B F = 2 O G $, $ O K // A B $, $ \therefore \angle K O G = \angle B A C = 60^{\circ} $, $ \therefore \triangle A F G $ 和 $ \triangle O K G $ 都是等边三角形, $ \angle O G D = \angle A F D = \angle B F R = 60^{\circ} $.
设 $ O K = x $, 则 $ O G = K G = x $, $ B F = 2 x $.
$ \because \angle B R F = \angle O Q G = 90^{\circ} $, $ \therefore \angle F B R = \angle G O Q = 30^{\circ} $, $ \therefore F R = \frac { 1 } { 2 } B F = x $, $ G Q = \frac { 1 } { 2 } O G = \frac { 1 } { 2 } x $,
$ \therefore B R = \sqrt { B F ^ { 2 } - F R ^ { 2 } } = \sqrt { ( 2 x ) ^ { 2 } - x ^ { 2 } } = \sqrt { 3 } x $, $ O Q = \sqrt { O G ^ { 2 } - G Q ^ { 2 } } = \sqrt { x ^ { 2 } - \left( \frac { 1 } { 2 } x \right) ^ { 2 } } = \frac { \sqrt { 3 } } { 2 } x $.
$ \because \frac { S _ { \triangle D O G } } { S _ { \triangle D B F } } = \frac { 3 } { 8 } $, $ \therefore \frac { \frac { 1 } { 2 } D G \cdot O Q } { \frac { 1 } { 2 } D F \cdot B R } = \frac { 3 } { 8 } $, 即 $ \frac { \frac { 1 } { 2 } D G \cdot \frac { \sqrt { 3 } } { 2 } x } { \frac { 1 } { 2 } D F \cdot \sqrt { 3 } x } = \frac { 3 } { 8 } $, $ \therefore \frac { D G } { D F } = \frac { 3 } { 4 } $, $ \therefore 4 D G = 3 D F $.
$ \because D F = 2 D K = 2 ( D G - x ) $, $ \therefore D G = 3 x $, $ D F = 4 x $.
在 $ \mathrm { Rt } \triangle D F T $ 中, $ \angle D F T = 60^{\circ} $, $ \angle D T F = 90^{\circ} $,
$ \therefore \angle F D T = 30^{\circ} $,
$ \therefore F T = \frac { 1 } { 2 } D F = 2 x $, $ \therefore D T ^ { 2 } = D F ^ { 2 } - F T ^ { 2 } = ( 4 x ) ^ { 2 } - ( 2 x ) ^ { 2 } = 12 x ^ { 2 } $.
$ \because A F = F G = F K - G K = \frac { 1 } { 2 } D F - G K = 2 x - x = x $,
$ \therefore A B = A F + B F = x + 2 x = 3 x $, $ A T = F T - A F = 2 x - x = x $.
在 $ \mathrm { Rt } \triangle A D T $ 中, $ A D = \sqrt { D T ^ { 2 } + A T ^ { 2 } } = \sqrt { 12 x ^ { 2 } + x ^ { 2 } } = \sqrt { 13 } x $, $ \therefore \frac { A D } { A B } = \frac { \sqrt { 13 } x } { 3 x } = \frac { \sqrt { 13 } } { 3 } $.