《2025年名校题库九年级数学全一册北师大版》

9. (成华区一诊)如图,在矩形 $ABCD$ 中,$AB = 2$,$AD = 3\sqrt{3}$,点 $E$ 在 $BC$ 边上,以 $AE$ 为边长在 $AE$ 右上方作等边 $\triangle AEF$,连接 $DF$。当点 $E$ 在 $BC$ 边上移动时,$DF$ 的取值范围是______。

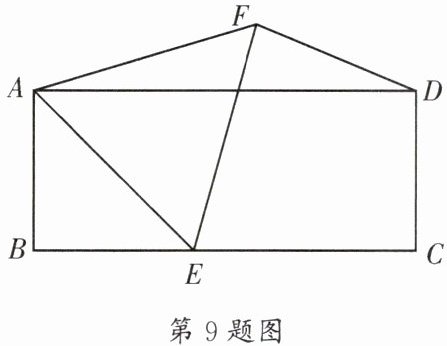
答案：
$\frac{5}{2}\leq DF\leq\sqrt{13}$
[解析]如图，以$AB$为边在$AB$右侧作等边$\triangle ABG$。$\because\triangle ABG$和$\triangle AEF$是等边三角形，$\therefore AB = AG$，$AE = AF$，$\angle BAG=\angle EAF$，$\therefore\angle BAG-\angle EAG=\angle EAF-\angle EAG$，即$\angle BAE=\angle GAF$，$\therefore\triangle ABE\cong\triangle AGF(SAS)$，$\therefore\angle AGF=\angle ABE = 90^{\circ}$，则点$F$在过点$G$且与$AG$垂直的直线上运动。连接$AC$，以$AC$为边在上方作等边$\triangle ACH$，$\therefore$点$F$在线段$GH$上运动。过点$D$作$GH$的垂线，垂足为$N$，令$GH$与$AD$交于点$M$，$\because AG = AB = 2$，且$\angle BAG = 60^{\circ}$，$\therefore\angle GAM = 30^{\circ}$，$\therefore MG=\frac{2\sqrt{3}}{3}$，$AM=\frac{4\sqrt{3}}{3}$。$\because AD = 3\sqrt{3}$，$\therefore DM=\frac{5\sqrt{3}}{3}$。由题易得$\triangle AGM\backsim\triangle DNM$，$\therefore\frac{AM}{DM}=\frac{AG}{DN}=\frac{GM}{NM}$，即$\frac{\frac{4\sqrt{3}}{3}}{\frac{5\sqrt{3}}{3}}=\frac{2}{DN}=\frac{\frac{2\sqrt{3}}{3}}{NM}$，$\therefore DN=\frac{5}{2}$，$MN=\frac{5\sqrt{3}}{6}$，即$DF$的最小值为$\frac{5}{2}$，$\therefore GN = GM + MN=\frac{2\sqrt{3}}{3}+\frac{5\sqrt{3}}{6}=\frac{3\sqrt{3}}{2}$。连接$GD$。在$Rt\triangle DNG$中，$DG=\sqrt{(\frac{5}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}=\sqrt{13}$。由题意，得$AC=\sqrt{31}$。又$AC = AH$，$\therefore AH=\sqrt{31}$。在$Rt\triangle AGH$中，$GH=\sqrt{(\sqrt{31})^{2}-2^{2}}=3\sqrt{3}$，$\therefore NH = 3\sqrt{3}-\frac{3\sqrt{3}}{2}=\frac{3\sqrt{3}}{2}$，则$NH = GN$。连接$DH$。又$\because DN\perp GH$，$\therefore DH = DG$，即$DF$的最大值为$\sqrt{13}$。故$\frac{5}{2}\leq DF\leq\sqrt{13}$。

10. (教科院附中)如图,在矩形 $ABCD$ 中,$AB = 6$,$BC = 8$,$E$ 为 $BC$ 上一点,且 $BE = 2$,$F$ 为 $AB$ 边上的一个动点,连接 $EF$,将 $EF$ 绕着点 $E$ 顺时针旋转 $30^{\circ}$ 到 $EG$ 的位置,连接 $FG$ 和 $CG$,则 $CG$ 的最小值为______。

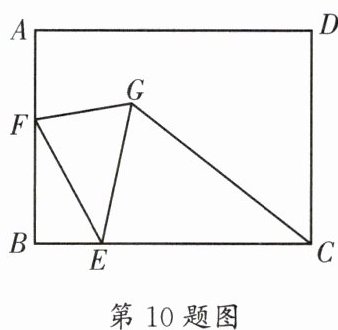
答案：
$3\sqrt{3}+2$
[解析]如图，将$BE$绕点$E$顺时针旋转$30^{\circ}$，得到$EH$，连接$HG$，过点$C$作$CP\perp GH$于点$P$，过点$E$作$EN\perp CP$于点$N$，$\therefore HE = BE = 2$。$\because$将$EF$绕着点$E$顺时针旋转$30^{\circ}$到$EG$的位置，$\therefore EF = EG$，$\angle FEG=\angle BEH = 30^{\circ}$，$\therefore\angle BEF=\angle HEG$。在$\triangle BEF$和$\triangle HEG$中，$\begin{cases}BE = HE,\\\angle BEF=\angle HEG,\\EF = EG,\end{cases}$$\therefore\triangle BEF\cong\triangle HEG(SAS)$，$\therefore\angle GHE=\angle B = 90^{\circ}$，点$G$在直线$HG$上运动，$\therefore$当$CG\perp HG$时，$CG$有最小值，最小值为$CP$的长。$\because CP\perp HG$，$\angle GHE = 90^{\circ}$，$\therefore CP// HE$，$\therefore\angle BCP=\angle BEH = 30^{\circ}$。$\because EN\perp CP$，$\therefore\angle PNE=\angle HEN = 90^{\circ}$，$\therefore$四边形$PNEH$是矩形，$\therefore PN = HE = 2$。$\because BC = 8$，$BE = 2$，$\therefore EC = 6$。$\because\angle BCP = 30^{\circ}$，$\angle ENC = 90^{\circ}$，$\therefore EN=\frac{1}{2}EC = 3$，$\therefore NC=\sqrt{3}EN = 3\sqrt{3}$，$\therefore CP = 3\sqrt{3}+2$，$\therefore CG$的最小值为$3\sqrt{3}+2$。

11. (郫都区一诊)如图,在菱形 $ABCD$ 中,$\angle A = 60^{\circ}$,点 $E$ 在对角线 $BD$ 上,且 $BE = 3DE$,$F$ 为边 $AB$ 上一动点,作 $\angle FEP = 60^{\circ}$,交 $BC$ 于点 $P$,交 $AB$ 的延长线于点 $G$。
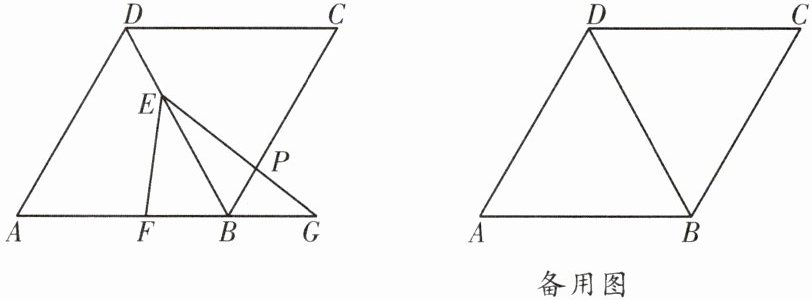
(1) 求证：$\triangle EFB\backsim\triangle GFE$；
(2) 连接 $PF$,求证：$\triangle EFP$ 是等边三角形；
(3) 连接 $PF$,延长 $FE$ 交 $CD$ 于点 $Q$,连接 $PQ$,当 $\triangle PEQ$ 与 $\triangle BFP$ 相似时,求 $\frac{EF}{EG}$ 的值。

答案：

(1)证明：$\because$四边形$ABCD$是菱形，$\therefore AD = AB$。$\because\angle A = 60^{\circ}$，$\therefore\triangle ABD$为等边三角形，$\therefore\angle ABD = 60^{\circ}$，$\therefore\angle G+\angle BEP = 60^{\circ}$。$\because\angle FEP = 60^{\circ}=\angle BEF+\angle BEP$，$\therefore\angle BEF=\angle G$。又$\because\angle BFE=\angle EFG$，$\therefore\triangle EFB\backsim\triangle GFE$。
(2)证明：方法一：如图1，过点$E$作$EM// AD$交$AB$于点$M$，则$\angle EMF=\angle A = 60^{\circ}$。

由
(1)可知$\angle EBM = 60^{\circ}$，$\therefore\angle EBP = 60^{\circ}$，$\triangle EBM$是等边三角形，$\therefore EM = EB$，$\angle MEB = 60^{\circ}$。$\because\angle FEP = 60^{\circ}$，$\therefore\angle MEF=\angle BEP$。在$\triangle EMF$和$\triangle EBP$中，$\begin{cases}\angle MEF=\angle BEP,\\EM = EB,\\\angle EMF=\angle EBP,\end{cases}$$\therefore\triangle EMF\cong\triangle EBP(ASA)$，$\therefore EF = EP$，$\therefore\triangle EFP$是等边三角形。
方法二：如图2，过点$E$作$EM\perp AB$于点$M$，作$EN\perp BC$于点$N$，则$\angle EMB=\angle ENB = 90^{\circ}$。

$\because$四边形$ABCD$是菱形，$\therefore BD$平分$\angle ABC$，$\angle ABC = 120^{\circ}$，$\therefore EM = EN$。$\because\angle FEP = 60^{\circ}$，$\therefore\angle ABC+\angle FEP = 180^{\circ}$，$\therefore\angle EFM+\angle EPB = 180^{\circ}$。$\because\angle EPN+\angle EPB = 180^{\circ}$，$\therefore\angle EFM=\angle EPN$。在$\triangle EFM$和$\triangle EPN$中，$\begin{cases}\angle EFM=\angle EPN,\\\angle EMF=\angle ENP,\\EM = EN,\end{cases}$$\therefore\triangle EFM\cong\triangle EPN(AAS)$，$\therefore EF = EP$，$\therefore\triangle EFP$是等边三角形。
(3)解：如图3，过点$E$作$EM// AD$交$AB$于点$M$。

设$DE = 1$，$FM = x$，则$BE = 3$。$\because\triangle ABD$是等边三角形，$\therefore AM = 1$，$BM = 3$，$\therefore BF = 3 - x$。由
(2)知$\triangle EMF\cong\triangle EBP$，$\therefore BP = FM = x$。$\because DC// BF$，$\therefore\frac{QE}{EF}=\frac{DE}{BE}=\frac{1}{3}$。$\because EF = EP$，$\therefore\frac{QE}{EP}=\frac{1}{3}$。$\because\angle FEP = 60^{\circ}$，$\therefore\angle PEQ = 120^{\circ}=\angle PBF$，$\therefore$当$\triangle PEQ$与$\triangle BFP$相似时可以分两种情况讨论：
①若$\triangle PEQ\backsim\triangle FBP$，此时$\frac{QE}{PB}=\frac{EP}{BF}=\frac{QP}{FP}$，$\therefore\frac{QE}{EP}=\frac{PB}{BF}=\frac{1}{3}$，$\therefore\frac{x}{3 - x}=\frac{1}{3}$，解得$x=\frac{3}{4}$。由
(1)知$\triangle EFB\backsim\triangle GFE$，$\therefore\frac{EF}{EG}=\frac{BF}{BE}=\frac{3 - x}{3}=\frac{3}{4}$。
②若$\triangle PEQ\backsim\triangle PBF$，此时$\frac{QE}{PE}=\frac{BF}{PB}=\frac{1}{3}$，即$\frac{3 - x}{x}=\frac{1}{3}$，解得$x=\frac{9}{4}$，$\therefore\frac{EF}{EG}=\frac{BF}{BE}=\frac{3 - x}{3}=\frac{1}{4}$。
综上所述，$\frac{EF}{EG}$的值为$\frac{3}{4}$或$\frac{1}{4}$。