《2025年名校题库九年级数学全一册北师大版》

3.(实外)【定义】平行四边形一组邻边的中点与不在这组邻边上的顶点顺次连接而成的三角形如果是直角三角形,那么称这个三角形为平行四边形的"中直三角形".
【初步感知】(1)如图1,四边形ABCD为矩形,$\triangle BEF$为其"中直三角形",其中$∠BEF= 90^{\circ }$,求$\frac {AD}{AB}$的值;
【深入探究】(2)如图2,$\triangle CEF为□ ABCD$的"中直三角形",其中$∠CFE= 90^{\circ },∠B= 60^{\circ }$,求$\frac {AD}{AB}$的值;
【拓展延伸】(3)在$\triangle ABC$中,$∠A= 90^{\circ },\frac {AB}{AC}= \frac {4}{3}$,以$\triangle ABC$为"中直三角形"的平行四边形的一组邻边的长记为m,n,其中$m＞n$,请直接写出$\frac {m}{n}$的值.

答案：
解:
(1)
∵四边形ABCD是矩形,
∴∠A = ∠D = 90°,AB = CD,
∴∠ABE + ∠AEB = 90°.
∵∠BEF = 90°,
∴∠AEB + ∠DEF = 90°,
∴∠ABE = ∠DEF,
∴△ABE∽△DEF,
∴$\frac{DE}{AB}$=$\frac{DF}{AE}$.
∵E是AD的中点,F是CD的中点,
∴DE = AE=$\frac{1}{2}AD$,DF = CF=$\frac{1}{2}CD=\frac{1}{2}AB$,
∴$\frac{\frac{1}{2}AD}{AB}$=$\frac{\frac{1}{2}AB}{\frac{1}{2}AD}$,
∴$\frac{AD}{AB}$=$\sqrt{2}$.
(2)如图1,过点C作CG⊥AD于点G,过点E作EH⊥AD,交DA的延长线于点H.

由
(1)知,$\frac{CG}{FH}$=$\frac{FG}{EH}$.
∵四边形ABCD是平行四边形,
∴AB//CD,AB = CD,∠D = ∠B = 60°,
∴∠HAE = ∠D = 60°,
∴$CG=\frac{\sqrt{3}}{2}CD=\frac{\sqrt{3}}{2}AB$,$DG=\frac{1}{2}CD=\frac{1}{2}AB$,$AH=\frac{1}{2}AE=\frac{1}{4}AB$,$EH=\frac{\sqrt{3}}{2}AE=\frac{\sqrt{3}}{4}AB$,
∴$FH = AF + AH=\frac{1}{2}AD+\frac{1}{4}AB$,$FG = DF - DG=\frac{1}{2}AD - \frac{1}{2}AB$,
∴$\frac{\frac{\sqrt{3}}{2}AB}{\frac{1}{2}AD+\frac{1}{4}AB}$=$\frac{\frac{1}{2}AD-\frac{1}{2}AB}{\frac{\sqrt{3}}{4}AB}$,化简得$2AD^{2}-AD\cdot AB - 4AB^{2}=0$,
∴$\frac{AD}{AB}$=$\frac{1+\sqrt{33}}{4}$或$\frac{AD}{AB}$=$\frac{1-\sqrt{33}}{4}$(舍去).
(3)如图2,△ABC是▱CDFE的“中直三角形”，过点B作BH⊥DF,交DF的延长线于点H,过点C作CG⊥DF于点G,
∴∠BHF = ∠CGD = 90°.

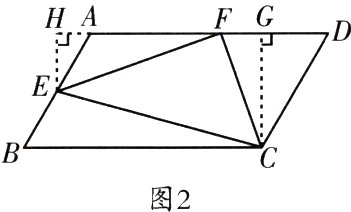
∵CD//EF,
∴∠D = ∠BFH,
∴△CDG∽△BFH,
∴$\frac{DG}{FH}$=$\frac{CG}{BH}$=$\frac{CD}{BF}$=$\frac{CD}{\frac{1}{2}EF}$=$\frac{EF}{\frac{1}{2}EF}$ = 2.
设FH = x,BH = y,则DG = 2x,CG = 2y.
由
(1)知,△ACG∽△BAH,
∴$\frac{AG}{BH}$=$\frac{CG}{AH}$ = $\frac{AC}{AB}$=$\frac{3}{4}$,
∴$AG=\frac{3}{4}BH=\frac{3}{4}y$,$AH=\frac{4}{3}CG=\frac{8}{3}y$,
∴$AF = AH - FH=\frac{8}{3}y - x$,$AD = DG + AG = 2x+\frac{3}{4}y$.
∵AF = AD,
∴$\frac{8}{3}y - x = 2x+\frac{3}{4}y$,
∴$x=\frac{23}{36}y$,
∴$AD = 2x+\frac{3}{4}y=\frac{73}{36}y$.
∵$BF=\sqrt{BH^{2}+FH^{2}}=\sqrt{y^{2}+(\frac{23}{36}y)^{2}}=\frac{5\sqrt{73}}{36}y$,
∴$\frac{m}{n}$=$\frac{2AD}{2BF}$=$\frac{AD}{BF}$=$\frac{\frac{73}{36}y}{\frac{5\sqrt{73}}{36}y}$=$\frac{\sqrt{73}}{5}$.
如图3,过点B作BG⊥DF于点G,过点C作CH⊥DF,交DF的延长线于点H.

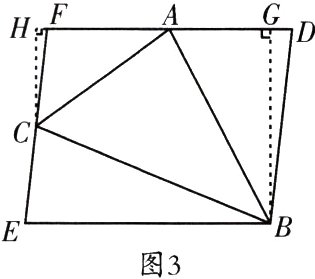
设FH = x,CH = y,则DG = 2x,BG = 2y.
由
(1)知,△ABG∽△CAH,
∴$\frac{AG}{CH}$=$\frac{BG}{AH}$ = $\frac{AB}{AC}$=$\frac{4}{3}$,
∴$AG=\frac{4}{3}CH=\frac{4}{3}y$,$AH=\frac{3}{4}BG=\frac{3}{2}y$,
∴$AF = AH - FH=\frac{3}{2}y - x$,$AD = AG + DG=\frac{4}{3}y + 2x$.
∵AF = AD,
∴$\frac{3}{2}y - x = \frac{4}{3}y + 2x$,
∴$y = 18x$,
∴$AD=\frac{4}{3}×18x + 2x = 26x$,$CF=\sqrt{FH^{2}+CH^{2}}=\sqrt{x^{2}+(18x)^{2}} = 5\sqrt{13}x$,
∴$\frac{m}{n}$=$\frac{2AD}{2CF}$=$\frac{AD}{CF}$=$\frac{26x}{5\sqrt{13}x}$=$\frac{2\sqrt{13}}{5}$.
如图4,过点E作EQ⊥AF于点Q,过点B作BH⊥AF于点H,过点C作CG⊥AF,交FA的延长线于点G.

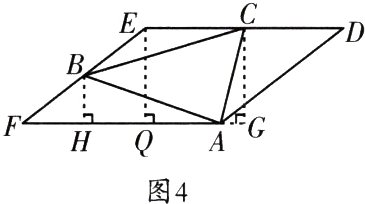
设BH = 4a,CE = CD = x,BF = BE = y,则CG = EQ = 2BH = 8a,AF = DE = 2CE = 2x.
由
(1)可知,△BHA∽△AGC,
∴$\frac{BH}{AG}$=$\frac{AH}{CG}$ = $\frac{AB}{AC}$=$\frac{4}{3}$,
∴$AG=\frac{3}{4}BH = 3a$,$AH=\frac{4}{3}CG=\frac{32}{3}a$,
∴$AQ = QG - AG = CE - AG = x - 3a$,
∴$HQ = AH - AQ=\frac{32}{3}a-(x - 3a)=\frac{41}{3}a - x$,$FH = AF - AH = 2x-\frac{32}{3}a$.
∵FH = HQ,
∴$2x-\frac{32}{3}a=\frac{41}{3}a - x$,
∴$x=\frac{73}{9}a$,
∴$FH=\frac{41}{3}a-\frac{73}{9}a=\frac{50}{9}a$,
∴$BF = \sqrt{FH^{2}+BH^{2}}=\sqrt{(\frac{50}{9}a)^{2}+(4a)^{2}}=\frac{2\sqrt{949}}{9}a$,
∴$\frac{m}{n}$=$\frac{CE}{BF}$=$\frac{\frac{73}{9}a}{\frac{2\sqrt{949}}{9}a}$=$\frac{\sqrt{949}}{26}$.
综上所述,$\frac{m}{n}$=$\frac{\sqrt{73}}{5}$或$\frac{2\sqrt{13}}{5}$或$\frac{\sqrt{949}}{26}$.