《2025年名校题库九年级数学全一册北师大版》

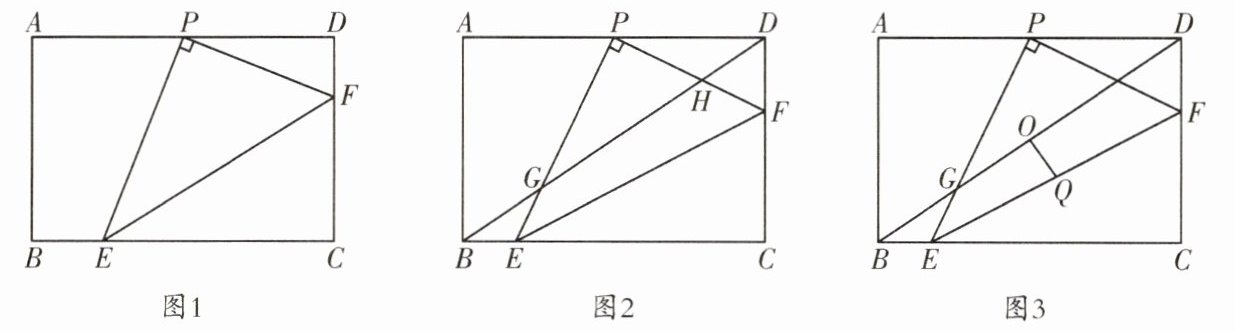
12. (青羊区一诊)在矩形 $ABCD$ 中,$AB = 4$,$BC = 6$,$P$ 为 $AD$ 边上的中点,$F$ 为 $CD$ 边上的动点且不与端点重合,连接 $PF$,过点 $P$ 作 $PE\perp PF$ 交 $BC$ 边于点 $E$,连接 $EF$。
(1) 如图 1,求 $\frac{PE}{PF}$ 的值。
(2) 如图 2,连接 $BD$ 分别交 $PE$,$PF$ 于点 $G$,$H$,若 $\triangle BEG\backsim\triangle DHP$,求 $BE$ 的长度。
(3) 如图 3,连接 $BD$,$O$ 为 $BD$ 的中点,$Q$ 为 $EF$ 的中点,连接 $OQ$。
① 当 $OQ\perp BD$ 时,求 $DF$ 的长度；
② 直接写出 $OQ$ 的取值范围。

答案：
解：
(1)如图1，过点$E$作$EN\perp AD$于点$N$。

$\because PE\perp PF$，即$\angle EPF = 90^{\circ}$，$\therefore\angle NPE+\angle DPF = 180^{\circ}-\angle EPF = 90^{\circ}$。$\because\angle D = 90^{\circ}$，$\therefore\angle PFD+\angle DPF = 90^{\circ}$，$\therefore\angle NPE=\angle PFD$。$\because\angle ENP=\angle D = 90^{\circ}$，$\therefore\triangle ENP\backsim\triangle PDF$，$\therefore\frac{PE}{PF}=\frac{NE}{PD}$。$\because NE = CD = 4$，$PD=\frac{1}{2}AD = 3$，$\therefore\frac{PE}{PF}=\frac{4}{3}$。
(2)如图2，过点$E$作$EN\perp AD$于点$N$，交$BD$于点$M$。

$\because\triangle BEG\backsim\triangle DHP$，$\therefore\angle DPH=\angle BGE$。$\because\angle DPH=\angle NEP$，$\therefore\angle BGE=\angle NEP$，$\therefore MG = ME$。$\because NE// CD$，$\therefore\triangle BEM\backsim\triangle BCD$，$\therefore\frac{ME}{BE}=\frac{CD}{BC}=\frac{4}{6}=\frac{2}{3}$。设$ME = 2k$，则$BE = 3k$，$MG = 2k$，$BM=\sqrt{13}k$，$\therefore\frac{BE}{BG}=\frac{3k}{\sqrt{13}k + 2k}=\frac{\sqrt{13}-2}{3}$。$\because AD// BC$，$\therefore\triangle PDG\backsim\triangle EBG$，$\therefore\frac{PD}{DG}=\frac{BE}{BG}=\frac{\sqrt{13}-2}{3}$。由$PD = 3$，可得$DG=\sqrt{13}+2$。在$Rt\triangle BCD$中，$BD=\sqrt{BC^{2}+CD^{2}}=\sqrt{6^{2}+4^{2}}=2\sqrt{13}$，$\therefore BG = (\sqrt{13}+2)k = BD - DG = 2\sqrt{13}-(2+\sqrt{13})=\sqrt{13}-2$，$\therefore k=\frac{\sqrt{13}-2}{\sqrt{13}+2}=\frac{17 - 4\sqrt{13}}{9}$，$\therefore BE = 3k=\frac{17 - 4\sqrt{13}}{3}$。
(3)①如图3，连接$DE$，取$DE$的中点$T$，连接$OT$，$QT$，则$OT// BE$且$OT=\frac{1}{2}BE$，$TQ// DF$且$TQ=\frac{1}{2}DF$。

$\because BC\perp CD$，$\therefore TO\perp TQ$。设$DF = x$，则$TQ=\frac{1}{2}x$。由
(1)可得$OT=\frac{1}{2}BE=\frac{1}{2}(3-\frac{4x}{3})=\frac{3}{2}-\frac{2}{3}x$。$\because OQ\perp BD$，$\therefore\angle DOT+\angle TOQ = 90^{\circ}$。又$\because\angle OQT+\angle TOQ = 90^{\circ}$，$\therefore\angle DOT=\angle OQT$。$\because\angle DOT=\angle DBC$，$\therefore\angle OQT=\angle DBC$。又$\because\angle OTQ=\angle BCD = 90^{\circ}$，$\therefore\triangle OTQ\backsim\triangle DCB$，$\therefore\frac{OT}{TQ}=\frac{CD}{BC}=\frac{4}{6}=\frac{2}{3}$，$\therefore\frac{\frac{3}{2}-\frac{2}{3}x}{\frac{1}{2}x}=\frac{2}{3}$，解得$x=\frac{3}{2}$，$\therefore DF=\frac{3}{2}$。
②$OQ=\sqrt{OT^{2}+QT^{2}}=\sqrt{\frac{25}{36}x^{2}-2x+\frac{9}{4}}=\sqrt{\frac{25}{36}(x-\frac{36}{25})^{2}+\frac{81}{100}}$，$\therefore$当$x=\frac{36}{25}$时，$OQ$有最小值$\frac{9}{10}$，当点$F$与点$D$重合时，$OQ$的值为$\frac{3}{2}$。$\because$点$F$不与点$D$重合，$\therefore\frac{9}{10}\leq OQ\lt\frac{3}{2}$。