《2025年名校题库九年级数学全一册北师大版》

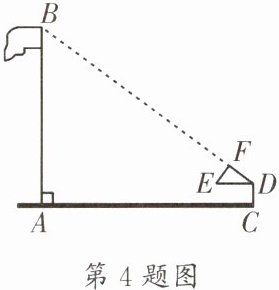
4. (成华区一诊)如图, 小明同学用木棍制成的$Rt\triangle DEF测量旗杆的高度AB$. 他调整自己的位置, 使斜边$DE保持与地面AC$平行, 直角边$DF与点B$在同一直线上. 已知$DF= 2$米, $EF= 1.5$米, 斜边$DE离地面的高度DC= 1.5$米, $AC= 14$米, 则旗杆的高度$AB= $12米.

答案： 12

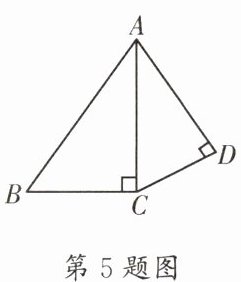
5. (师大一中)如图, 已知$\angle ACB= \angle ADC= 90^{\circ}, AD= 2, CD= \sqrt{2}$, 当$AB$的长为3或3$\sqrt{2}$时, $\triangle ACB与\triangle ADC$相似.

答案： 3或3$\sqrt{2}$

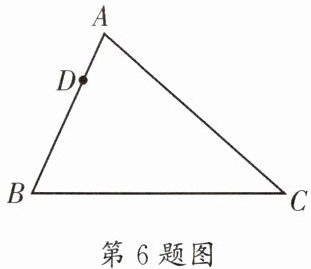
6. (龙泉驿区一诊)如图, 在$\triangle ABC$中, $AB= 6, AC= 8$, $D是边AB$上一点, 且$AD= 2$, 如果点$E在边AC$上, 且$\triangle ADE与\triangle ABC$相似, 那么$AE$的长为$\frac{8}{3}$或$\frac{3}{2}$.

答案： $\frac{8}{3}$或$\frac{3}{2}$

7. (七中育才)如图, 在$Rt\triangle ABC$中, $\angle BAC= 90^{\circ}$, 按以下步骤作图: ①以点$A$为圆心, 适当长为半径画弧, 分别交$AB, AC于点M, N$; ②再分别以点$M, N$为圆心, 大于$\frac{1}{2}MN$的长为半径画弧, 两弧交于点$O$, 连接$AO并延长交BC于点D$; ③分别以点$A, D$为圆心, 大于$\frac{1}{2}AD$的长为半径画弧, 两弧分别交于$P, Q$两点, 作直线$PQ$, 分别交$AB, AC于点E, F$. 若$AB= 3, AC= 4$, 则$AE$的长为______.

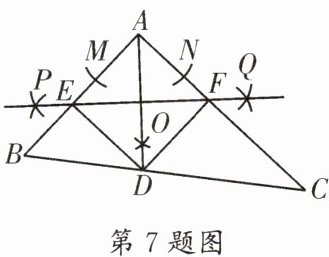
答案：
$\frac{12}{7}$　[解析]由作法得EF垂直平分AD,AD平分∠BAC,如图，设PQ交AD于点G.
∵EF垂直平分AD,
∴EA=ED,AG⊥EF,FA=FD,
∴∠EDA=∠EAD.
∵AD平分∠BAC，
∴
∠EAD=∠FAD.在△AGF和△AGE中，$\begin{cases} \angle AGF = \angle AGE = 90^{\circ}, \\ AG = AG, \\ \angle FAG = \angle EAG, \end{cases}$
∴△AGF≌△AGE（ASA）,
∴AF=AE,
∴AE=DE=FD=AF,
∴四边形AEDF是菱形.
∵∠BAC=90°,
∴四边形AEDF是正方形,
∴DE//AC,DF//AB,
∴∠BDE=∠C,∠BED=∠BAC=∠DFC=90°,
∴△BED∽△DFC,
∴$\frac{BE}{FD}=\frac{DE}{CF}$.设正方形
AEDF的边长为x，
∴BE=3−x,CF=4−x,
∴$\frac{3−x}{x}=\frac{x}{4−x}$,解得x=$\frac{12}{7}$,即AE=$\frac{12}{7}$.
　　　　　

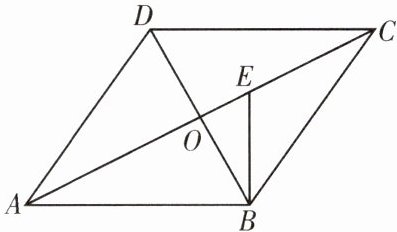
8. (七中育才)如图, 在菱形$ABCD$中, 对角线$AC, BD$相交于点O, $EB\perp AB$, 垂足为$B$, 交$AC于点E$.
(1)求证: $\frac{OE}{OB}= \frac{BE}{BC}$;
(2)若$AE= 6, AB= 5$, 求$EC$的长.

(1)证明:∵四边形ABCD为菱形，∴AC⊥BD,AB=BC.
　∵EB⊥AB,∴∠EOB=∠EBA.
　∵∠OEB=∠BEA,∴△EOB∽△EBA,∴$\frac{OE}{OB}=\frac{BE}{AB}$.
　∵AB=BC,∴$\frac{OE}{OB}=\frac{BE}{BC}$.
　(2)解:∵∠AOB=∠ABE=90°,∠OAB=∠BAE,∴△AOB∽△ABE,∴$\frac{OA}{AB}=\frac{AB}{AE}$.
　∵AE=6,AB=5,∴$\frac{OA}{5}=\frac{5}{6}$,解得OA=$\frac{25}{6}$,∴EC=2OA−AE=$\frac{25}{3}$−6=$\frac{7}{3}$.

答案：
(1)证明:
∵四边形ABCD为菱形，
∴AC⊥BD,AB=BC.
∵EB⊥AB,
∴∠EOB=∠EBA.
∵∠OEB=∠BEA,
∴△EOB∽△EBA,
∴$\frac{OE}{OB}=\frac{BE}{AB}$.
∵AB=BC,
∴$\frac{OE}{OB}=\frac{BE}{BC}$.
(2)解:
∵∠AOB=∠ABE=90°,∠OAB=∠BAE,
∴△AOB∽△ABE,
∴$\frac{OA}{AB}=\frac{AB}{AE}$.
∵AE=6,AB=5,
∴$\frac{OA}{5}=\frac{5}{6}$,解得OA=$\frac{25}{6}$,
∴EC=2OA−AE=$\frac{25}{3}$−6=$\frac{7}{3}$.

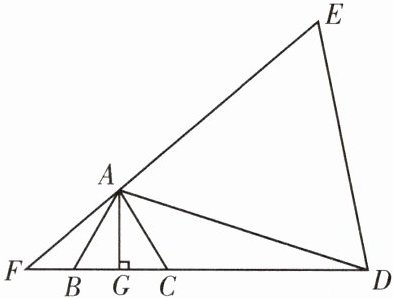
9. (武侯区一诊)如图, 已知$\triangle ABC$是等边三角形, 点$D在边BC$的延长线上, 连接$AD$, 以$AD为边在直线AD的右侧作等边\triangle ADE$, 延长$EA交直线BC于点F$.
(1)求证: $\triangle FAB\backsim\triangle ADC$;
(2)过点$A作AG\perp BC于点G$, 若$CG= \sqrt{3}, AD= 2\sqrt{21}$, 求$CD, AF$的长.

答案：

(1)证明:如图,连接CE.
∵△ABC,△ADE都是等边三角形,
∴AB=AC,AD=AE,∠ABC=∠ACB=∠BAC=∠EAD=60°,
∴∠ABF=∠ACD=120°,∠BAD=∠EAC,
∴△ABD≌△ACE(SAS),
∴∠ACE=∠ABC=60°=∠BAC,∠ADB=∠AEC,
∴AB//CE,
∴∠FAB=∠AEC=∠ADB,
∴△FAB∽△ADC;
　　　　　
(2)解:
∵△ABC是等边三角形，AG⊥BC,CG=$\sqrt{3}$,
∴AC=AB=BC=2$\sqrt{3}$,AG=3.
在Rt△AGD中，由勾股定理可得，DG=$\sqrt{AD^{2}-AG^{2}}=5\sqrt{3}$,
∴CD=4$\sqrt{3}$
∵△FAB∽△ADC,
∴$\frac{FA}{AD}=\frac{AB}{CD}$,即$\frac{FA}{2\sqrt{21}}=\frac{2\sqrt{3}}{4\sqrt{3}}$,
∴FA=$\sqrt{21}$