第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
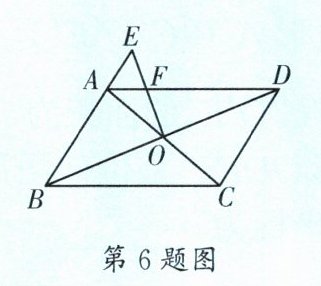
6.(成华区一诊)如图,在$□ ABCD$中,对角线$AC$,$BD相交于点O$,在$BA的延长线上取一点E$,连接$OE交AD于点F$.若$CD= 5$,$BC= 8$,$AE= 2$,则$AF= $____.

答案:
$\frac{16}{9}$ [解析]如图,过点O作OM//AD交AB于点M.
∵四边形ABCD是平行四边形,
∴OM//AD//BC,OB=OD,
∴AM=BM=$\frac{1}{2}$AB=$\frac{5}{2}$,OM=$\frac{1}{2}$BC=4.
∵AF//OM,
∴△AEF∽△MEO,
∴$\frac{AE}{EM}=\frac{AF}{OM}$,
∴$\frac{2}{2 + \frac{5}{2}}=\frac{AF}{4}$,
∴AF=$\frac{16}{9}$.

$\frac{16}{9}$ [解析]如图,过点O作OM//AD交AB于点M.
∵四边形ABCD是平行四边形,
∴OM//AD//BC,OB=OD,
∴AM=BM=$\frac{1}{2}$AB=$\frac{5}{2}$,OM=$\frac{1}{2}$BC=4.
∵AF//OM,
∴△AEF∽△MEO,
∴$\frac{AE}{EM}=\frac{AF}{OM}$,
∴$\frac{2}{2 + \frac{5}{2}}=\frac{AF}{4}$,
∴AF=$\frac{16}{9}$.

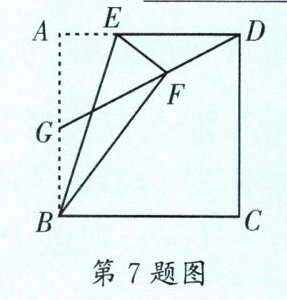
7.(龙泉驿区一诊)如图,在正方形$ABCD$中,$AB= 2$,$E为AD$上一动点,将三角形$ABE沿BE$折叠,点$A落在点F$处,连接$DF$并延长,与边$AB交于点G$.若$G为AB$的中点,则$AE$的长为
$\frac{2}{3}$
.
答案:
$\frac{2}{3}$
8.(成华区一诊)如图,在矩形$ABCD$中,延长$BC到点E$,延长$CB到点F$,使$BF= CE$,$AE与DF交于点G$.
(1)求证:$GE= GF$;
(2)过点$E作EF$的垂线,交$FD的延长线于点H$,若$\frac {AB}{HE}= \frac {3}{4}$,$AD= 4$,求$CE$的长.
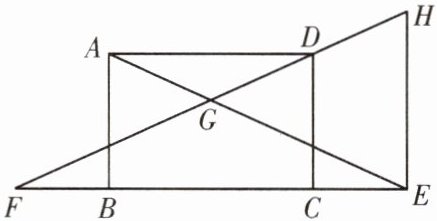
(1)证明:∵四边形ABCD是矩形,∴∠ABE =∠DCF=90°,AB=DC.
∵BF=CE,∴BF+BC=CE+BC,即CF=BE.
在△ABE和△DCF中,$\begin{cases} AB = DC, \\ \angle ABE = \angle DCF, \\ BE = CF, \end{cases}$
∴△ABE≌△DCF(SAS),∴∠AEB=∠DFC,∴GE=GF.
(2)解:∵四边形ABCD是矩形,∴AB=DC,BC=AD=4,∠DCB=90°,即DC⊥EF.
又∵HE⊥EF,∴DC//HE,∴△CDF∽△EHF,∴$\frac{DC}{HE}=\frac{CF}{EF}$,∴$\frac{AB}{HE}=\frac{BC + BF}{BC + BF + CE}$。∵BF = CE,$\frac{AB}{HE} = \frac{3}{4}$,∴$\frac{4 + CE}{4 + 2CE} = \frac{3}{4}$,解得CE =
(1)求证:$GE= GF$;
(2)过点$E作EF$的垂线,交$FD的延长线于点H$,若$\frac {AB}{HE}= \frac {3}{4}$,$AD= 4$,求$CE$的长.

(1)证明:∵四边形ABCD是矩形,∴∠ABE =∠DCF=90°,AB=DC.
∵BF=CE,∴BF+BC=CE+BC,即CF=BE.
在△ABE和△DCF中,$\begin{cases} AB = DC, \\ \angle ABE = \angle DCF, \\ BE = CF, \end{cases}$
∴△ABE≌△DCF(SAS),∴∠AEB=∠DFC,∴GE=GF.
(2)解:∵四边形ABCD是矩形,∴AB=DC,BC=AD=4,∠DCB=90°,即DC⊥EF.
又∵HE⊥EF,∴DC//HE,∴△CDF∽△EHF,∴$\frac{DC}{HE}=\frac{CF}{EF}$,∴$\frac{AB}{HE}=\frac{BC + BF}{BC + BF + CE}$。∵BF = CE,$\frac{AB}{HE} = \frac{3}{4}$,∴$\frac{4 + CE}{4 + 2CE} = \frac{3}{4}$,解得CE =
2
。
答案:
(1)证明:
∵四边形ABCD是矩形,
∴∠ABE =∠DCF=90°,AB=DC.
∵BF=CE,
∴BF+BC=CE+BC,即CF=BE.
在△ABE和△DCF中,$\begin{cases} AB = DC, \\ \angle ABE = \angle DCF, \\ BE = CF, \end{cases}$
∴△ABE≌△DCF(SAS),
∴∠AEB=∠DFC,
∴GE=GF.
(2)解:
∵四边形ABCD是矩形,
∴AB=DC,BC=AD=4,∠DCB=90°,即DC⊥EF.
又
∵HE⊥EF,
∴DC//HE,
∴△CDF∽△EHF,
∴$\frac{DC}{HE}=\frac{CF}{EF}$,
∴$\frac{AB}{HE}=\frac{BC + BF}{BC + BF + CE}$。
∵BF = CE,$\frac{AB}{HE} = \frac{3}{4}$,
∴$\frac{4 + CE}{4 + 2CE} = \frac{3}{4}$,解得CE = 2。
(1)证明:
∵四边形ABCD是矩形,
∴∠ABE =∠DCF=90°,AB=DC.
∵BF=CE,
∴BF+BC=CE+BC,即CF=BE.
在△ABE和△DCF中,$\begin{cases} AB = DC, \\ \angle ABE = \angle DCF, \\ BE = CF, \end{cases}$
∴△ABE≌△DCF(SAS),
∴∠AEB=∠DFC,
∴GE=GF.
(2)解:
∵四边形ABCD是矩形,
∴AB=DC,BC=AD=4,∠DCB=90°,即DC⊥EF.
又
∵HE⊥EF,
∴DC//HE,
∴△CDF∽△EHF,
∴$\frac{DC}{HE}=\frac{CF}{EF}$,
∴$\frac{AB}{HE}=\frac{BC + BF}{BC + BF + CE}$。
∵BF = CE,$\frac{AB}{HE} = \frac{3}{4}$,
∴$\frac{4 + CE}{4 + 2CE} = \frac{3}{4}$,解得CE = 2。
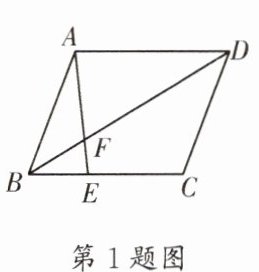
1. (成外)如图,在$□ ABCD$中,$E是BC$上的一点,且$BE:EC= 2:3$,$AE交BD于点F$,则$BF:FD$等于(
A. $2:5$
B. $3:5$
C. $2:3$
D. $5:7$
A
)
A. $2:5$
B. $3:5$
C. $2:3$
D. $5:7$
答案:
A
2. (高新区期末)小孔成像的原理是光的直线传播.如图,一发光的电子蜡烛$AB$(竖直放置)经小孔$O$在屏幕(竖直放置)上成像$A'B'$.若$AB= 24cm$,$A'B'= 8cm$,小孔$O到AB的距离为45cm$,则小孔$O到A'B'$的距离为______
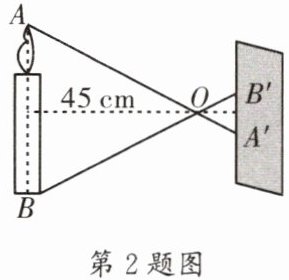
15
$cm$.
答案:
15
查看更多完整答案,请扫码查看


