《2025年名校题库九年级数学全一册北师大版》

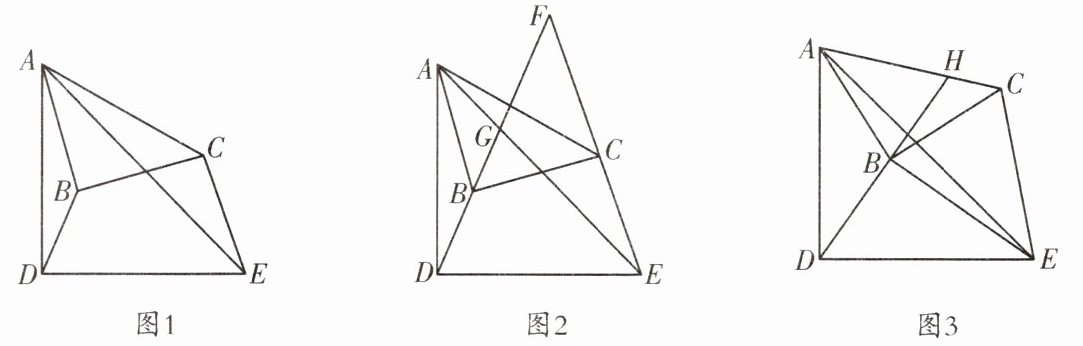
5. (天府新区一诊)如图 1,已知$△ABC\backsim △ADE,AB= BC,\frac {AB}{AC}= \frac {5}{7}$,连接 BD,CE.
【尝试初探】(1)当$△ABC$绕点 A 旋转过程中,试探究$\frac {BD}{CE}$的值；
【深入探究】(2)如图 2,点 B 在$△ADE$内部,延长 DB 交 EC 的延长线于点 F,交 AE 于点 G,若$DG= 3,GF= 2$,求 AE 的长；
【拓展延伸】(3)如图 3,点 B 在$△ADE$内部,连接 BE,延长 DB 交 AC 于点 H,若$∠CEA= ∠BED,BE= 5,BH= 3$,且$∠BCE＜90^{\circ }$,求 CE 的长.

答案：
解:
(1)
∵△ABC∽△ADE,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$,∠BAC=∠DAE,
∴$\frac{AB}{AC}$=$\frac{AD}{AE}$=$\frac{5}{7}$,∠EAC=∠DAB,
∴△DAB∽△EAC,
∴$\frac{BD}{CE}$=$\frac{AD}{AE}$=$\frac{5}{7}$.
(2)
∵△DAB∽△EAC,
∴∠ADB=∠AEC;又
∵∠AGD=∠FGE,
∴∠GAD=∠F.
∵△ABC∽△ADE,AB=BC,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$=$\frac{BC}{DE}$,
∴AD=DE,
∴∠DAE=∠AED,
∴∠DEG=∠F.
∵∠GDE=∠EDF,
∴△GDE∽△EDF,
∴$\frac{DG}{DE}$=$\frac{DE}{DF}$,
∴DE²=DG.DF=3×(3+2)=15,
∴AD=DE=　$\sqrt{15}$，
∵$\frac{AD}{AE}$=$\frac{5}{7}$，
∴AE=$\frac{7\sqrt{15}}{5}$.
(3)
∵∠CEA=∠BED,
∴∠CEB=∠AED.
∵∠DAE=∠AED,∠BAC=∠DAE,
∴∠BAC=∠CEB.
∵△DAB∽△EAC,
∴∠ABD=∠ACE,
∴∠BAH+∠AHB=∠ACB+∠BCE.
∵AB=BC,
∴∠BAH=∠ACB,
∴∠AHB =∠BCE,
∴△AHB∽△ECB,
∴$\frac{AB}{EB}$=$\frac{BH}{BC}$=$\frac{AH}{CE}$,即$\frac{AB}{5}$=$\frac{3}{BC}$,
∴AB=BC=　$\sqrt{15}$,
∴$\frac{\sqrt{15}}{5}$=$\frac{AH}{CE}$.
∵$\frac{AB}{AC}$=$\frac{5}{7}$，
∴AC=$\frac{7\sqrt{15}}{5}$.
如图，过点B作BK⊥AC于点K.

∵AB=BC,
∴AK=$\frac{1}{2}AC$=$\frac{7\sqrt{15}}{10}$.
∵BK²=AB²−AK²,KH²=BH²−BK²=9−BK²,
∴BK²=$\frac{153}{20}$,KH²=$\frac{27}{20}$,
∴KH=$\frac{3\sqrt{15}}{10}$,
∴AH=AK+KH=$\frac{7\sqrt{15}}{10}$+$\frac{3\sqrt{15}}{10}$=　$\sqrt{15}$,
∴CE=5.