第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
5. (武侯区一诊)若$\frac {a}{b}= \frac {c}{d}= \frac {e}{f}= \frac {1}{2}$,其中$b+2d-f= 8$,则$a+2c-e$的值为______
4
。
答案:
4
6. (树德实验)已知实数$a$,$b$,$c满足\frac {1}{a+1}= \frac {2}{b+2}= \frac {3}{c-3}$,则$a-2b+c$的值为______
6
。
答案:
6
7. (石室联中)已知$a:b:c= 2:3:5$。
(1)求代数式$\frac {3a-b+c}{2a+3b-c}$的值;
(2)如果$3a-b+c= 48$,求$a$,$b$,$c$的值。
(1)求代数式$\frac {3a-b+c}{2a+3b-c}$的值;
1
(2)如果$3a-b+c= 48$,求$a$,$b$,$c$的值。
$a=12$,$b=18$,$c=30$
答案:
解: $\because a:b:c = 2:3:5$,
$\therefore$ 设 $a = 2k$, $b = 3k$, $c = 5k(k \neq 0)$.
(1) $\frac{3a - b + c}{2a + 3b - c} = \frac{6k - 3k + 5k}{4k + 9k - 5k} = 1$.
(2) $3a - b + c = 6k - 3k + 5k = 48$, 解得 $k = 6$,
$\therefore a = 2k = 12$, $b = 3k = 18$, $c = 5k = 30$.
$\therefore$ 设 $a = 2k$, $b = 3k$, $c = 5k(k \neq 0)$.
(1) $\frac{3a - b + c}{2a + 3b - c} = \frac{6k - 3k + 5k}{4k + 9k - 5k} = 1$.
(2) $3a - b + c = 6k - 3k + 5k = 48$, 解得 $k = 6$,
$\therefore a = 2k = 12$, $b = 3k = 18$, $c = 5k = 30$.
1.(天府新区一诊)如图,点 C 是线段 AB 的黄金分割点$(AC>BC)$,则下列结论中正确的是 (

A.$AB^{2}= AC^{2}+BC^{2}$
B.$BC^{2}= AC\cdot BA$
C.$\frac {BC}{AC}= \frac {\sqrt {5}-1}{2}$
D.$\frac {AC}{BC}= \frac {\sqrt {5}-1}{2}$
C
)
A.$AB^{2}= AC^{2}+BC^{2}$
B.$BC^{2}= AC\cdot BA$
C.$\frac {BC}{AC}= \frac {\sqrt {5}-1}{2}$
D.$\frac {AC}{BC}= \frac {\sqrt {5}-1}{2}$
答案:
C
2.(高新区期末)如图,在$△ABC$中,$AB= AC,∠BAC= 36^{\circ }$,以点 C 为圆心,BC 的长为半径作弧,交 AC 于点 D,再分别以点 B,D 为圆心,大于$\frac {1}{2}BD$的长为半径作弧,两弧相交于点 F,作射线 CF 交 AB 于点 E,连接 DE,则以下结论不正确的是 (
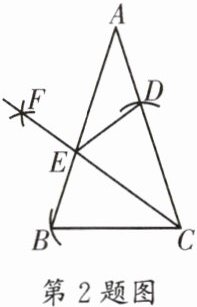
A.$∠BCE= 36^{\circ }$
B.$AD= BE$
C.$\frac {BE}{AB}= \frac {\sqrt {5}-1}{2}$
D.$CE^{2}= AD\cdot AC$
C
)
A.$∠BCE= 36^{\circ }$
B.$AD= BE$
C.$\frac {BE}{AB}= \frac {\sqrt {5}-1}{2}$
D.$CE^{2}= AD\cdot AC$
答案:
C
3.(武侯区一诊)在如图所示的“五角星”图案中,C,D 两点都是线段 AB 的黄金分割点.若$AC= 4$,则线段 AB 的长为
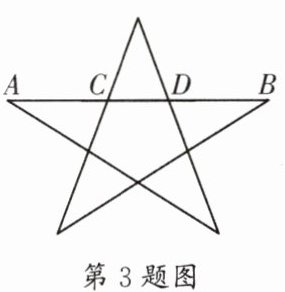
$ 6 + 2 \sqrt { 5 } $
.(结果保留根号)
答案:
$ 6 + 2 \sqrt { 5 } $
4.(天府七中)黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱.摄影中有一种拍摄手法叫黄金构图法,其原理是:如图,将正方形 ABCD 的底边 BC 取中点 E,以点 E 为圆心,线段 DE 的长为半径作圆弧,与底边 BC 的延长线交于点 F,这样就把正方形 ABCD 延伸为矩形 ABFG,称其为黄金矩形.若$CF= 4a$,则$AB= $____
$ ( 2 + 2 \sqrt { 5 } ) a $
.
答案:
$ ( 2 + 2 \sqrt { 5 } ) a $
5.(武侯区一诊)在一次趣味运动会中,某数学项目小组利用黄金分割比$\frac {\sqrt {5}-1}{2}$设计了一个掷飞镖的游戏.如图,在$△ABC$“靶”中,M,N 分别是线段 BC 的两个黄金分割点,我们把$△AMN$的内部称为“黄金区域”(图中阴影部分).游戏规定:投掷的飞镖落在“黄金区域”即为获胜.假设投掷的飞镖都能落在“靶”内,现小明随机向该“靶”投掷一枚飞镖,则小明获胜的概率是
$\sqrt{5}-2$
.
答案:
$ \sqrt { 5 } - 2 $
查看更多完整答案,请扫码查看


