《2025年名校题库九年级数学全一册北师大版》

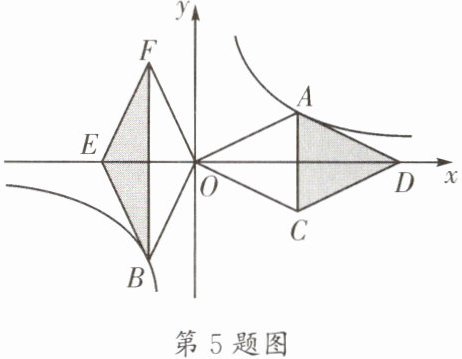
5. (郫都区一诊)如图,在平面直角坐标系 $ xOy $ 中,点 $ A $、点 $ B $ 都在双曲线 $ y = \frac{k}{x} $ 上,点 $ D $、点 $ E $ 都在 $ x $ 轴上,并且四边形 $ OADC $ 和四边形 $ OBEF $ 都是菱形. 若两个阴影部分的面积和为 8,则 $ k $ 的值为______4.

答案： 4

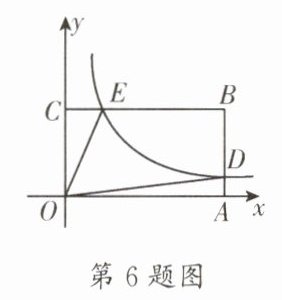
6. (金牛区一诊)如图,在以 $ O $ 为原点的平面直角坐标系中,点 $ A,C $ 分别在 $ x $ 轴、$ y $ 轴的正半轴上,点 $ B $ 在第一象限内,四边形 $ OABC $ 是矩形,反比例函数 $ y = \frac{k}{x}(x \gt 0) $ 的图象与 $ AB $ 相交于点 $ D $,与 $ BC $ 相交于点 $ E $. 若 $ BE = 4CE $,四边形 $ ODBE $ 的面积是 8,则 $ k = $______2.

答案： 2 【解析】设点E(a,$\frac{k}{a}$)，则点B(5a,$\frac{k}{a}$)，则S四边形CDBE=S矩形ABCO−S△OCE−S△AOD=5a·$\frac{k}{a}$−$\frac{1}{2}$k−$\frac{1}{2}$k=8，解得k=2.

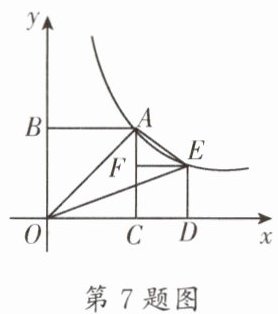
7. (武侯区一诊)如图,正方形 $ ABOC $ 与正方形 $ EFCD $ 的边 $ OC,CD $ 均在 $ x $ 轴上,点 $ F $ 在 $ AC $ 边上,反比例函数 $ y = \frac{k}{x}(x \gt 0) $ 的图象经过点 $ A,E $,且 $ S_{\triangle OAE} = 3 $,则 $ k = $______6.

答案： 6 【解析】设点A(a,a)，点E(a+b,b)，则AC=a，CD=DE=b.
∵S梯形ACDE=S△AOE+S△BOD−S△AOC=S△AOE+$\frac{1}{2}$|k|−$\frac{1}{2}$|k|=S△AOE，
∴$\frac{1}{2}$(a+b)b=$\frac{1}{2}$|k|=3，
∴k=6.

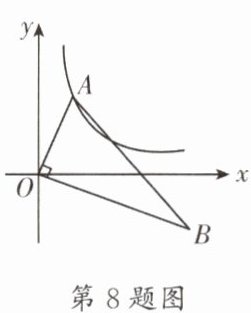
8. (高新区一诊)如图,在 $ Rt \triangle AOB $ 中,$ O $ 为坐标原点,$ \angle AOB = 90^{\circ} $,$ \angle B = 30^{\circ} $. 若点 $ A $ 在反比例函数 $ y = \frac{1}{x}(x \gt 0) $ 的图象上运动,点 $ B $ 在反比例函数 $ y = \frac{k}{x}(x \gt 0) $ 的图象上运动,则 $ k = $______.

答案：
−3 【解析】如图，分别过点A，B作AC⊥y轴于点C，BD⊥y轴于点D，则△OAC∽△BOD，
∴$\frac{S_{△OAC}}{S_{△OBD}}=(\frac{OA}{OB})^{2}=(\frac{1}{\sqrt{3}})^{2}=\frac{1}{3}$，
∴S△OBD=3S△OAC，
∴$\frac{1}{2}$|k|=3×$\frac{1}{2}$×1，
∴k=±3.又
∵k＜0，
∴k=−3.

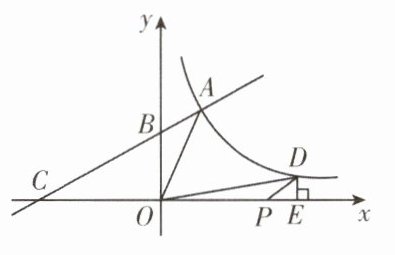
9. (新都区二诊)如图,点 $ A(2,n) $ 和点 $ D $ 是反比例函数 $ y = \frac{m}{x}(m \gt 0,x \gt 0) $ 图象上的两点,一次函数 $ y = kx + 3(k \neq 0) $ 的图象经过点 $ A $,与 $ y $ 轴、$ x $ 轴分别交于点 $ B $ 和点 $ C $,过点 $ D $ 作 $ DE \perp x $ 轴,垂足为 $ E $,连接 $ OA,OD $,已知 $ \triangle OAB $ 与 $ \triangle ODE $ 的面积满足 $ S_{\triangle OAB}:S_{\triangle ODE} = 3:4 $.
(1)求 $ S_{\triangle OAB} $ 与反比例函数的表达式；
$ S_{\triangle OAB} $=3，反比例函数的表达式为$ y = \frac{8}{x} $.
(2)已知点 $ P(6,0) $ 在线段 $ OE $ 上,当 $ \angle PDE = \angle CBO $ 时,求点 $ D $ 的坐标.
点 $ D $ 的坐标为(8,1).

答案： 解:
(1)当x=0时，y=kx+3=3，
∴B(0,3).
∵点A的坐标是(2,n)，
∴S△OAB=$\frac{1}{2}$×3×2=3.
∵S△OAB:S△CDE=3:4，
∴S△CDE=4.
∵D是反比例函数y=$\frac{m}{x}$(m＞0,x＞0)图象上的点，
∴$\frac{1}{2}$m=S△CDE=4，
∴m=8，
∴反比例函数的表达式为y=$\frac{8}{x}$.
(2)由
(1)知点A(2,n)在反比例函数y=$\frac{8}{x}$的图象上，
∴2n=8，
∴n=4，
∴A(2,4).
将点A的坐标(2,4)代入y=kx+3，得2k+3=4，解得k=$\frac{1}{2}$，
∴直线AC的表达式为y=$\frac{1}{2}$x+3.令y=$\frac{1}{2}$x+3=0，解得x=−6，
∴C(−6,0)，
∴OC=6.
由
(1)知OB=3，设D(a,b)，则ab=8，DE=b，PE=a-6.
∵∠PDE=∠CBO，∠COB=∠PED=90°，
∴△CBO∽△PDE，
∴$\frac{OB}{DE}=\frac{OC}{PE}$，即$\frac{3}{b}=\frac{6}{a-6}$.
又
∵ab=8，
∴$\begin{cases}a=-2\\b=-4\end{cases}$(舍去)或$\begin{cases}a=8\\b=1\end{cases}$
∴D(8,1).