《2025年名校题库九年级数学全一册北师大版》

8. (武侯区一诊)已知关于 $ x $ 的一元二次方程 $ x^{2} + mx + n = 0 $,现从 $ - 2 $,$ 1 $,$ 2 $ 这三个数中任取一个数作为方程中 $ m $ 的值,再从剩下的两个数中任取一个数作为方程中 $ n $ 的值,则取得的 $ m $,$ n $ 的值能使该一元二次方程有实数根的概率是______$\frac{2}{3}$。

答案： $\frac{2}{3}$

9. (师大一中考)如果 $ m $ 是从 $ - 3 $,$ - 2 $,$ - 1 $,$ 0 $,$ 1 $,$ 2 $,$ 3 $ 这七个数中任取的一个数,那么关于 $ x $ 的方程 $ \frac{m}{x - 3} = \frac{2}{x - 3} + 1 $ 的根为正数的概率为$\frac{3}{7}$。

答案： $\frac{3}{7}$

10. (嘉祥)从 $ - 2 $,$ - 1 $,$ 0 $,$ \frac{1}{3} $,$ 1 $,$ 2 $ 这六个数字中随机抽取一个数记为 $ a $,则使得关于 $ x $ 的方程 $ \frac{ax + 2}{x - 3} = 1 $ 的解为非负数,且满足关于 $ x $ 的不等式组 $ \begin{cases} x - a ＞ 0, \\ - 3 + 2x \leq 1 \end{cases} $ 只有三个整数解的概率是$\frac{1}{6}$。

答案： $\frac{1}{6}$

11. (新都区期末)从 $ 2 $,$ 0 $,$ - 1 $,$ - 2 $,$ - 3 $ 这五个数中,随机抽取一个数作为 $ m $ 的值,则使函数 $ y = (m^{2} - 6)x $ 的图象经过第二、四象限,且使关于 $ x $ 的一元二次方程 $ (m + 1)x^{2} + mx + 1 = 0 $ 有实数根的概率是$\frac{1}{5}$。

答案： $\frac{1}{5}$

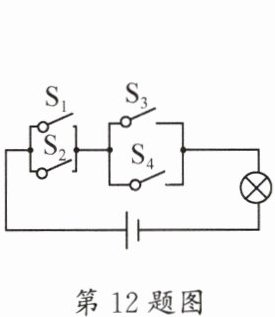
12. (成华区一诊)如图所示的电路中,随机闭合开关 $ S_{1} $,$ S_{2} $,$ S_{3} $,$ S_{4} $ 中的两个,能够点亮灯泡的概率为$\frac{2}{3}$。

答案： $\frac{2}{3}$

13. (温江区二诊)已知关于 $ x $ 的方程 $ x^{2} - 2mx + m^{2} - m - 1 = 0 $ 的两根分别为 $ x_{1} $,$ x_{2} $,且 $ x_{1} + x_{2} - x_{1}x_{2} = 1 $。如果把 $ m $ 的值作为点 $ P $ 的横坐标,点 $ P $ 的纵坐标是从 $ - 2 $,$ - 1 $,$ 0 $,$ 1 $,$ 2 $,$ 3 $ 这 $ 6 $ 个数中任意取出的一个数,则得到的点 $ P $ 在第四象限的概率为$\frac{1}{6}$。

答案： $\frac{1}{6}$

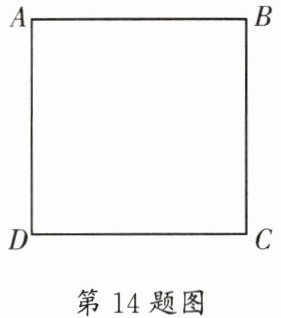
14. (金牛区一诊)如图,正方形的边长为 $ 1 $ 个单位长度,将一枚棋子按顺时针方向依次沿正方形 $ ABCD $ 的四个顶点移动。每次开始时,棋子都位于点 $ A $ 处；然后,掷两枚质地均匀的骰子,掷得的点数之和是几就移动棋子几个单位长度,如掷得的点数之和为 $ 3 $ 就移动 $ 3 $ 步落在点 $ D $ 处,掷得的点数之和为 $ 6 $ 就移动 $ 6 $ 步落在点 $ C $ 处……掷一次骰子,棋子落在点 $ B $ 处的概率是______$\frac{2}{9}$。

答案： $\frac{2}{9}$

15. (锦江区一诊)如图所示,两个矩形 $ A $ 和 $ B $,若矩形 $ B $ 的周长是矩形 $ A $ 的周长的 $ k $ 倍,矩形 $ B $ 的面积也是矩形 $ A $ 的面积的 $ k $ 倍,则称 $ k $ 为矩形 $ B $ 相对于矩形 $ A $ 的“共比系数”。若 $ n = 2 $ 时,矩形 $ B $ 相对于矩形 $ A $ 的“共比系数”为 $ \frac{9}{7} $,则 $ a = $$\frac{6}{7}$或3；若 $ 1 \leq m \leq 5 $,$ 8 \leq n \leq 10 $($ m $,$ n $ 均为正整数),则矩形 $ B $ 相对于矩形 $ A $ 的“共比系数”为 $ \frac{1}{m} $ 的概率为$\frac{7}{15}$。

答案： $\frac{6}{7}$或3　$\frac{7}{15}$