《2025年名校题库九年级数学全一册北师大版》

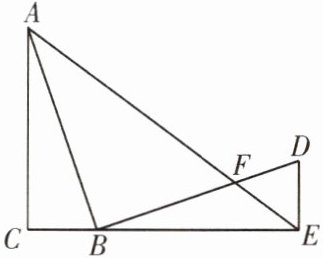
5. (成华区一诊)数学综合与实践小组的同学对“一线三直角”图形进行了深入研究。如图,在$△ABC$中,$∠C= 90^{\circ }$,$BC= 2$,$AC= 6$,将斜边AB绕点B顺时针旋转$90^{\circ }$得到线段BD,过点D作BC的垂线,交直线BC于点E。
【初步感知】(1)求CE的长；
【深入研究】(2)连接AE交BD于点F,求BF的长；
【拓展延伸】(3)若点P在直线BC上,满足$∠PAB= 30^{\circ }$,请直接写出线段BP的长。

答案：
解:
(1)由旋转得AB=BD,∠ABD=90°,
∴∠ABC+∠DBE=90°.
∵DE⊥BC,
∴∠DEB=90°.
∵∠C=90°,
∴∠C=∠DEB,∠CAB+∠ABC=90°,
∴∠DBE=∠CAB.在△ACB和△BED中，{∠CAB = ∠EBD,∠C = ∠DEB,AB = BD},
∴△ACB≌△BED(AAS),
∴BE=AC=6,CB=DE=2,
∴CE=BC+BE=2+6=8.
(2)解法一:如图1,延长AC,DB交于点M.

∵∠ACB=90°,
∴∠BCM=90°=∠DEB.
∵∠DBE=∠CBM,
∴△CBM∽△EBD,
∴CM/DE=BC/BE.
∵BC=DE=2,BE=6,
∴CM/2=2/6,
∴CM=2/3.由勾股定理，得BM=√BC²+CM²=√2²+(2/3)²=2√10/3,BD=√BE²+DE²=√6²+2²=2√10,
∴DM=BM+BD=2√10/3+2√10=8√10/3.
∵∠BCM=∠DEB,
∴AM//DE,
∴△AMF∽△EDF,
∴FM/DF=AM/DE,
∴FM/DF=(6 + 2/3)/2=10/3,
∴DF=3/10FM,
∴DF=3/13DM=8√10/3×3/13=8√10/13,
∴BF=BD−DF=2√10−8√10/13=18√10/13.
解法二:如图2,过点F作FN⊥CE于点N.

∵∠C=∠BNF=90°,∠CAB=∠NBF,
∴△ACB∽△BNF,
∴AC/CB=BN/FN=6/2=3.设FN=a,则BN=3a.
∵FN//AC,
∴△EFN∽△EAC,
∴FN/AC=EN/CE,即a/6=EN/8,
∴EN=4a/3.
∵BE=BN+EN=6,
∴3a+4a/3=6,
∴a=18/13,
∴BF=√10a=18√10/13.
(3)分两种情况:
①当点P在点C的左边时,如图3,过点P作PG⊥AB于点G.

∵∠PAG=30°,∠AGP=90°,
∴PG=1/2AP.设PG=x,则AP=2x,
∴AG=√3x.
∵S△APB=1/2PB·AC=1/2AB·PG,
∴1/2×6×PB=1/2×2√10x,
∴PB=√10x/3.由勾股定理，得BG=√PB²−PG²=√(√10x/3)²−x²=1/3x.
∵BG=AB−AG,
∴1/3x=2√10 - √3x,解得x=(9√30 - 3√10)/13,
∴PB=√10x/3=(30√3 - 10)/13.
②当点P在点B的右边时,如图4,设AP交BD于点O,过点O作OG⊥CE于点G.

在Rt△ABO中,∠BAO=30°,AB=2√10,
∴OB=2√10/√3=2√30/3.
∵∠OBG=∠BAC,∠C=∠OGB=90°,
∴△ACB∽△BGO,
∴AC/BG=CB/OG=AB/OB,
∴6/BG=2/OG=2√10/(2√30/3)=√3,
∴BG=2√3,OG=2√3/3.
∵OG//AC,
∴△POG∽△PAC,
∴OG/AC=PG/PC,
∴(2√3/3)/6=PG/(2 + 2√3 + PG),
∴PG=(4√3 + 10)/13,
∴PB=PG+BG=(4√3 + 10)/13+2√3=(30√3 + 10)/13.综上所述，PB的长是(30√3 - 10)/13或(30√3 + 10)/13.