《2025年名校题库九年级数学全一册北师大版》

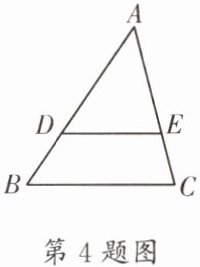
4. (石室联中)如图,在$\triangle ABC$中,$DE// BC$,$AB= 9$,$BD= 3$,$AE= 4$,则$EC$的长为______2。

答案： 2

5. (金牛区期末)如图,菱形$ABCD的边长为6cm$,$\angle BAD= 60^{\circ }$,将菱形沿射线$AC方向平移得到四边形A'B'C'D'$,$A'D'交CD于点E$。若$DC= 3DE$,则平移的距离为______$cm$。

答案：
$2\sqrt{3}$ [解析]如图，连接 $BD$ 交 $AC$ 于点 $O$，过点 $E$ 作 $EF \perp AC$ 于点 $F$。$\because$ 四边形 $ABCD$ 是菱形，$\therefore AD = AB = CD = 6\mathrm{cm}$，$AO = CO$，$OB = OD$，$BD \perp AC$，$\angle BCD = \angle BAD = 60^{\circ}$，$\therefore \triangle ABD$ 是等边三角形，$\angle DAC = \angle DCA = \frac{1}{2}\angle BCD = 30^{\circ}$，$\therefore BD = AB = 6\mathrm{cm}$，$\therefore OB = \frac{1}{2}BD = 3\mathrm{cm}$，$\therefore AO = CO = \sqrt{3}OB = 3\sqrt{3}\mathrm{cm}$，$\therefore AC = 2AO = 6\sqrt{3}\mathrm{cm}$。$\because DC = 3DE = 6\mathrm{cm}$，$\therefore DE = 2\mathrm{cm}$，$\therefore CE = DC - DE = 4\mathrm{cm}$。由平移的性质得 $\angle EA'F = 30^{\circ} = \angle DCA$，$\therefore A'E = CE$。$\because EF \perp AC$，$\therefore \angle EFC = 90^{\circ}$，$A'F = CF$，$\therefore EF = \frac{1}{2}CE = 2\mathrm{cm}$，$\therefore CF = \sqrt{3}EF = 2\sqrt{3}\mathrm{cm}$，$\therefore A'C = 2CF = 4\sqrt{3}\mathrm{cm}$，$\therefore AA' = AC - A'C = 6\sqrt{3} - 4\sqrt{3} = 2\sqrt{3}(\mathrm{cm})$，即平移的距离为 $2\sqrt{3}\mathrm{cm}$。

1. (嘉祥)如图,在$\triangle ABC$中,点 D 在 AC 边上,$AD:DC= 1:2$,O 是 BD 的中点,连接 AO 并延长交 BC 于点 E,则$BE:EC= $ ( )

A. $1:2$
B. $1:3$
C. $1:4$
D. $2:3$

答案：
B　[解析]如图，过点O作OG//BC交AC于点G,则DG=CG,BC=2OG.又
∵AD:DC=1:2,
∴$\frac{OG}{EC}$=$\frac{AG}{AC}$=$\frac{2}{3}$,
∴EC=$\frac{3}{2}$OG,
∴BE=BC−EC=$\frac{1}{2}$OG,
∴BE:EC=$\frac{1}{2}$OG:$\frac{3}{2}$OG=1:3.
　　　　　　　

2. (天府新区一诊)如图,AD 是$\triangle ABC$的中线,E 是 AD 上的一点,且$AE:ED= 1:2$,BE 的延长线交 AC 于点 F,则$AF:FC= $____.

答案：
1:4　[解析]如图,过点D作DH//BF交AC于点H.
∵AD是△ABC的中线，
∴$\frac{CH}{FH}$=$\frac{CD}{BD}$=1,
∴FH=HC.
∵DH//BF,
∴$\frac{AF}{FH}$=$\frac{AE}{ED}$=$\frac{1}{2}$,
∴AF:FC=1:4.
　　　　　　　

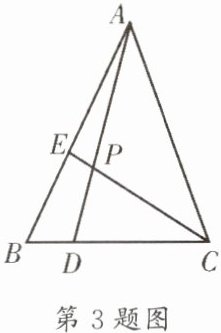
3. (温江区一诊)如图,D 是 BC 上的一点,E 是 AB 上的一点,AD,CE 交于点 P,且$AE:EB= 3:2,CP:CE= 5:6$,那么$DB:CD= $____.

答案：
1:3　[解析]如图,作EF//BC交AD于点F.
∵EF//BD,AE:EB=3:2,
∴EF:BD=AE:AB=3:5,
∴BD=$\frac{5}{3}$EF.
∵EF//CD,
∴EF:CD=EP:PC,而CP:CE=5:6,
∴EF:CD=1:5,
∴CD=5EF,
∴BD:CD=$\frac{5}{3}$EF:5EF=1:3.
　　　　　　

4. (锦江区一诊)如图,在四边形 ABCD 中,$AD// BC,AB⊥BC$,对角线 DB 平分$∠ADC$.过点 D 作$DE⊥BC$于点 E,BF 平分$∠DBC$交 DC 于点 F,交 DE 于点 G.若$BG= GF,BE= 1$,则 CD 的长为____.

答案：
$\frac{9+\sqrt{17}}{4}$　　[解析]
∵AD//BC,
∴∠ADB=∠DBC.
∵DB平分∠ADC，
∴∠ADB=∠CDB,
∴∠DBC=∠CDB,
∴CD=CB.如图，过点F作FH⊥BC于点H.
∵DE⊥BC,
∴FH//DE,
∴$\frac{BG}{BF}$=$\frac{BE}{BH}$.
∵BG=GF,
∴BE=EH=1,
∴BH=2.设CD=CB=x,x＞2,则CH=x−2,CE=x−1.在Rt△CDE中,DE²=CD²−CE²=x²−(x−1)²=2x−1.在Rt△BDE中,BD=$\sqrt{BE²+DE²}$=$\sqrt{2x}$.
∵FH//DE,
∴$\frac{DF}{CF}$=$\frac{EH}{CH}$=$\frac{1}{x−2}$.
∵BF平分∠DBC,
∴$\frac{BD}{BC}$=$\frac{DF}{CF}$，
∴$\frac{\sqrt{2x}}{x}$=$\frac{1}{x−2}$,解得x=$\frac{9+\sqrt{17}}{4}$或x=$\frac{9−\sqrt{17}}{4}$(舍去)，即CD=$\frac{9+\sqrt{17}}{4}$.
　　　　　　　

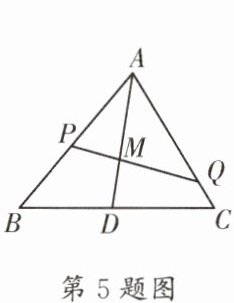
5. (金牛区一诊)如图,设 M 是$\triangle ABC$的重心,过点 M 的直线分别交 AB,AC 于点 P,Q,则$\frac {PB}{PA}+\frac {CQ}{QA}= $____.

答案：
1　　[解析]如图，分别过点B,C作BE//AD,CF//AD,分别交直线PQ于点E,F,则BE//AD//CF,
∴$\frac{ME}{MF}$=$\frac{BD}{CD}$=1,ME=MF,MD是梯形BCFE的中位线，
∴BE+CF=2MD.
∵M是△ABC的重心,
∴$\frac{AM}{MD}$=2,
∴$\frac{PB}{PA}$+$\frac{CQ}{QA}$=$\frac{BE}{AM}$+$\frac{CF}{AM}$=$\frac{BE + CF}{AM}$=$\frac{2MD}{AM}$=1.
　　　　　　

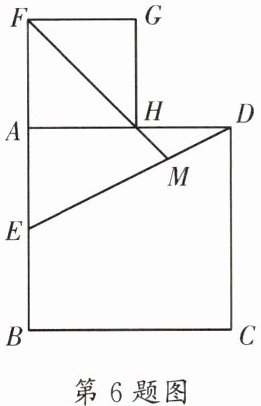
6. (高新区期末)如图,正方形 ABCD 的边长为 2,E 是 AB 的中点,连接 ED,延长 EA 至点 F,使$EF= ED$.以线段 AF 为边作正方形 AFGH,点 H 落在 AD 边上,连接 FH 并延长,交 ED 于点 M,则$\frac {DM}{DE}$的值为____.

答案：
$\frac{3-\sqrt{5}}{3}$　[解析]如图，过点M作MN⊥AD于点N.
∵正方形ABCD的边长为2,E是AB的中点，
∴AD=AB=2,AE=1,∠EAD=90°,
∴EF=DE=$\sqrt{AE²+AD²}$=$\sqrt{5}$.
∵四边形AFGH是正方形，
∴AH=AF=EF−AE=$\sqrt{5}$−1.
∵∠AHF=∠NHM=45°,
∴MN=NH.
∵MN//AE,
∴$\frac{MN}{AE}$=$\frac{DN}{DA}$=$\frac{DM}{DE}$，
∴$\frac{MN}{1}$=$\frac{DN}{2}$=$\frac{DM}{\sqrt{5}}$;设MN=NH=x,则DN=2x,DM=$\sqrt{5}$x,
∴DN+NH=AD−AH,
∴3x=2−($\sqrt{5}$−1)=3−$\sqrt{5}$,
∴x=$\frac{3-\sqrt{5}}{3}$，
∴$\frac{DM}{DE}$=$\frac{\sqrt{5}x}{\sqrt{5}}$=x=$\frac{3-\sqrt{5}}{3}$.