《2025年名校题库九年级数学全一册北师大版》

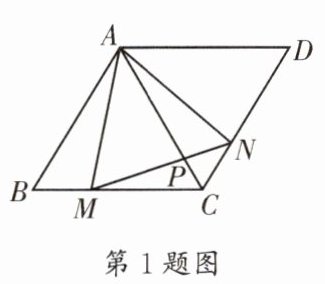
1.(金牛区二诊)如图,在边长为6的菱形ABCD中,AC为其对角线,$∠ABC= 60^{\circ }$,M,N分别是边BC,CD上的动点,且$MB= NC$,连接AM,AN,MN,MN交AC于点P,则点P到直线CD的距离的最大值为____$\frac{3\sqrt{3}}{4}$.

答案： $\frac{3\sqrt{3}}{4}$

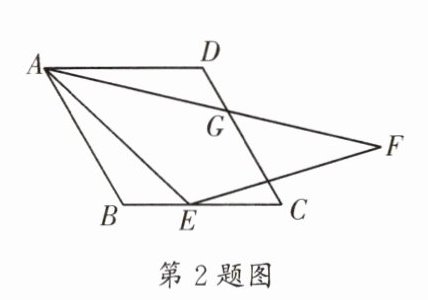
2.(师大一中)如图,在菱形ABCD中,$∠B= 120^{\circ }$,E是BC上一点,连接AE,将AE绕点E顺时针旋转$120^{\circ }$至FE,连接AF与CD相交于点G.若$\frac {DG}{CG}= \frac {1}{4}$,则$\frac {BE}{CE}= $____.

答案：
$\frac{4}{3}$ [解析]如图，延长AF交BC的延长线于点M，在CM上截取CN=BE，连接FN，FC，过点F作FH⊥CM于点H。
∵四边形ABCD是菱形，
∴AD//CM，AB=BC=AD，
∴△ADG∽△MCG，
∴$\frac{CM}{DA}=\frac{CG}{DG}=4$，即CM=4DA。设菱形ABCD的边长AD=BC=a，BE=x，则CM=4a，CE=a - x。由旋转可知EA=EF，∠AEF=120°，
∴∠FEN + ∠AEB = 60°。又
∵∠B = 120°，则∠EAB + ∠AEB = 60°，
∴∠EAB = ∠FEN。又
∵CN = BE，则EN = CN + EC = BE + EC = BC = AB，
∴△ABE≌△ENF(SAS)，
∴BE = NF = CN = x，∠FNE = ∠EBA = 120°，
∴∠FNH = 60°。
∵FH⊥CM，则∠NFH = 30°，
∴NH = $\frac{1}{2}$FN = $\frac{1}{2}$x，则FH = $\sqrt{FN^{2}-NH^{2}}=\frac{\sqrt{3}}{2}x$。
∵EA = EF，∠AEF = 120°，
∴∠EFA = ∠EAF = 30°，则∠EFM = 150°。
∵CN = NF，∠FNE = 120°，
∴∠FCN = ∠CFN = 30°，则∠ECF = 150°，则∠ECF = ∠EFM。又
∵∠CEF = ∠FEM，
∴△ECF∽△EFM，
∴$\frac{EC}{EF}=\frac{EF}{EM}$，即EC·EM = EF²，
∴(a - x)(5a - x) = ($\frac{\sqrt{3}}{2}$x)² + (a + $\frac{1}{2}$x)²，整理，得x² - 6ax + 5a² = x² + ax + a²，即4a² - 7ax = 0，则4a = 7x(a = 0舍去)，
∴x = $\frac{4}{7}$a，
∴BE = $\frac{4}{7}$a，则CE = BC - BE = a - $\frac{4}{7}$a = $\frac{3}{7}$a，
∴$\frac{BE}{CE}=\frac{\frac{4}{7}a}{\frac{3}{7}a}=\frac{4}{3}$。

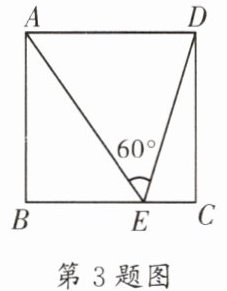
3.(嘉祥)如图,在矩形ABCD中,E是BC上一点,连接AE,DE.若$∠AED= 60^{\circ }$,且$BE= 2\sqrt {3}$,$EC= \sqrt {3}$,则矩形的边AB的长为____.

答案：
$\frac{3+\sqrt{33}}{2}$ [解析]如图，在CB的延长线上取一点F，连接AF，使∠F = 60°，在BC的延长线上取一点G，连接DG，使∠G = 60°，则∠F = ∠G = 60°。设BF = a。
∵四边形ABCD是矩形，
∴AB = DC，∠ABC = ∠DCB = 90°，
∴∠ABF = ∠DCG = 90°。在△ABF和△DCG中，$\begin{cases}∠ABF = ∠DCG\\∠F = ∠G\\AB = DC\end{cases}$，
∴△ABF≌△DCG(AAS)，
∴BF = CG = a，AF = DG。在Rt△ABF中，∠F = 60°，
∴∠FAB = 90° - ∠F = 30°，
∴AF = 2BF = 2a。由勾股定理得AB = $\sqrt{AF^{2}-BF^{2}}=\sqrt{3}a$，
∴DG = AF = 2a。
∵BE = 2$\sqrt{3}$，CE = $\sqrt{3}$，
∴EF = BF + BE = a + 2$\sqrt{3}$，EG = CG + EC = a + $\sqrt{3}$。在△AEF中，∠F = 60°，
∴∠AEF + ∠FAE = 120°。
∵∠AED = 60°，
∴∠AEF + ∠GED = 120°，
∴∠FAE = ∠GED。又
∵∠F = ∠G = 60°，
∴△FAE∽△GED，
∴$\frac{AF}{EG}=\frac{EF}{DG}$，
∴$\frac{2a}{a+\sqrt{3}}=\frac{a+2\sqrt{3}}{2a}$，整理得a² - $\sqrt{3}$a - 2 = 0，解得a₁ = $\frac{\sqrt{3}+\sqrt{11}}{2}$，a₂ = $\frac{\sqrt{3}-\sqrt{11}}{2}$(不合题意，舍去)，
∴a = $\frac{\sqrt{3}+\sqrt{11}}{2}$，
∴AB = $\sqrt{3}$a = $\sqrt{3}$×$\frac{\sqrt{3}+\sqrt{11}}{2}=\frac{3+\sqrt{33}}{2}$。

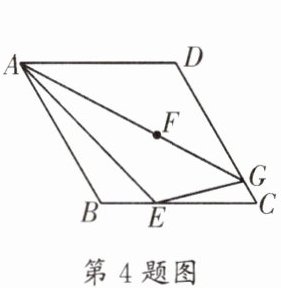
4.(高新区期末)如图,在菱形ABCD中,$∠ABC= 120^{\circ }$,点E在边BC上,$BE= 2$,连接AE,点B关于直线AE的对称点为F,射线AF交边DC于点G,连接EG.若$∠AEG= 120^{\circ }$,则线段AG的长为____.

答案：
$4\sqrt{2}+2$ [解析]
∵四边形ABCD是菱形，
∴AB = BC = CD，AB//CD，AD//BC。
∵∠ABC = 120°，
∴∠C = 60°。如图，连接EF。
∵点B关于直线AE的对称点为F，
∴△ABE≌△AFE，
∴BE = EF = 2，AB = AF，∠ABC = ∠AFE = 120°，∠BAE = ∠EAG。
∵∠AEG = ∠ABC = 120°，
∴∠AEB = ∠AGE。在EC上找一点M，连接MG，使∠EMG = 120°，在GF上截取GN = GM，连接EN。
∵∠AEC = ∠AEG + ∠CEG = ∠ABC + ∠BAE，
∴∠CEG = ∠BAE，
∴△ABE∽△EMG，
∴∠AEB = ∠EGM = ∠AGE。在△EMG和△ENG中，$\begin{cases}EG = EG\\∠EGM = ∠EGN\\GM = GN\end{cases}$，
∴△EMG≌△ENG(SAS)，
∴∠EMG = ∠ENG = 120°，EM = EN，
∴∠ENF = 180° - ∠ENG = 60°。
∵∠EFN = 180° - ∠AFE = 60°，
∴∠ENF = ∠EFN = 60°，
∴△ENF是等边三角形，
∴EF = FN = EN = 2，
∴EM = 2。
∵∠CMG = 180° - ∠EMG = 60° = ∠C，
∴△CMG是等边三角形，
∴设CM = CG = GM = a，则GN = a，BC = BE + EM + CM = 4 + a = AB。
∵△ABE∽△EMG，
∴$\frac{AB}{EM}=\frac{BE}{GM}$，即$\frac{4+a}{2}=\frac{2}{a}$，整理得a² + 4a - 4 = 0，解得a = 2$\sqrt{2}-2$(负值舍去)，
∴AG = AF + FN + GN = 4 + a + 2 + a = 4$\sqrt{2}+2$。

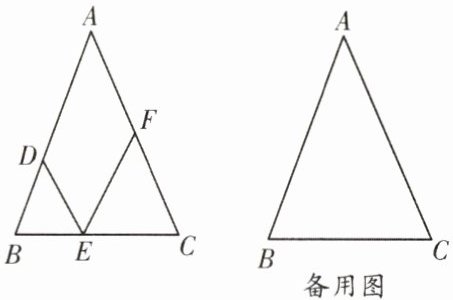
5.(西川)如图,在$△ABC$中,$AB= AC= 6$,$BC= 5$,D是AB上的一点,$BD= 2$,E是BC上的一动点,连接DE,并作$∠DEF= ∠B$,EF交线段AC于点F.
(1)求证：$△DBE\backsim △ECF$；
(2)当F是线段AC的中点时,求线段BE的长；
(3)连接DF,如果$△DEF与△DBE$相似,求FC的长.

答案：

(1)证明:
∵AB = AC = 6，
∴∠B = ∠C。又
∵∠B + ∠BDE = ∠DEC = ∠DEF + ∠FEC，∠DEF = ∠B，
∴∠BDE = ∠CEF，
∴△DBE∽△ECF。
(2)解:
∵△DBE∽△ECF，
∴$\frac{BD}{CE}=\frac{BE}{CF}$。
∵F是线段AC的中点，
∴CF = $\frac{1}{2}$AC = 3，
∴$\frac{2}{5-BE}=\frac{BE}{3}$，
∴BE = 2或3。
(3)解:
∵△DEF与△DBE相似，
∴∠BED = ∠EDF或∠BED = ∠DFE。
①当∠BED = ∠EDF时，DF//BC，
∴∠ADF = ∠B，∠AFD = ∠C，
∴∠ADF = ∠AFD，
∴AD = AF = 4，
∴CF = AC - AF = 2。
②当∠BED = ∠DFE时，
∵△DBE∽△ECF，
∴∠BED = ∠CFE，
∴∠DFE = ∠CFE，∠BDE = ∠FDE，
∴点E在∠BDF与∠DFC的平分线上。如图，过点E分别作EM⊥AB于点M，EN⊥AC于点N，EG⊥DF于点G，连接AE，

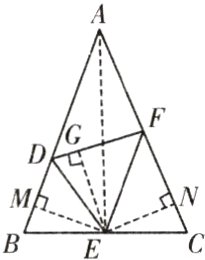
则EM = EG = EN，
∴AE是∠BAC的平分线，
∴BE = CE = $\frac{5}{2}$。
∵△DBE∽△ECF，
∴$\frac{BD}{CE}=\frac{BE}{CF}$，即$\frac{2}{\frac{5}{2}}=\frac{\frac{5}{2}}{CF}$，
∴CF = $\frac{25}{8}$。
综上所述，FC的长为2或$\frac{25}{8}$。