《2025年名校题库九年级数学全一册北师大版》

6. (高新区期末)
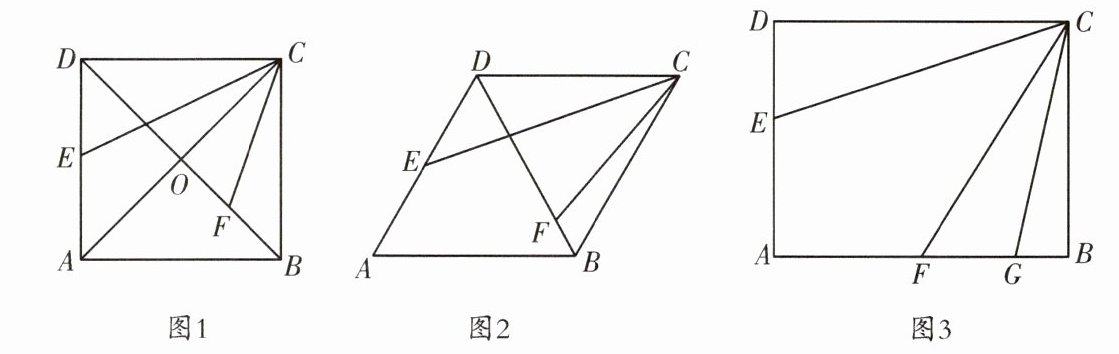
(1)基础：如图 1,在正方形 ABCD 中,点 E 在边 AD 上,点 F 在对角线 BD 上,连接 AC,CE,CF,AC 交 BD 于点 O.若$∠ECF= 45^{\circ }$,求证：$△CEA\backsim △CFB$.
(2)迁移：如图 2,在菱形 ABCD 中,$∠A= 60^{\circ },AB= 4\sqrt {3}$,E 为 AD 的中点,点 F 在对角线 BD 上.若$∠ECF= 30^{\circ }$,求线段 CF 的长.
(3)拓展：如图 3,在矩形 ABCD 中,$AB:BC= 4:3$,点 G 在边 AB 上,连接 CG,使得$AG= CG$,E,F 两点分别在线段 AD,AG 上,连接 CE,CF,且$∠ECF+\frac {1}{2}∠AGC= 90^{\circ }$.当$\frac {AE}{DE}= \frac {AF}{GF}= n$时,求 n 的值.

答案：

(1)证明:在正方形ABCD中，
∵OA=OD=OB=OC,∠AOD=∠BOC=90°,
∴∠OAD=∠OBC=∠OCB=45°.
∵∠ECF=45°,
∴∠OCB=∠ECF=45°,
∴∠OCB−∠OCF=∠ECF−∠OCF,即∠BCF=∠ACE.
∵∠EAC=∠FBC,
∴△CEA∽△CFB.
(2)解:如图1,连接AC,过点E作EH⊥CD,交CD的延长线于点H,交AC于点M,则∠HED =∠AEM=∠EAM=30°,
∴∠EMC=60°.

在菱形ABCD中，∠ABC=120°，
∴∠DBC=60°,∠ACB=30°,
∴∠EMC=∠DBC=60°.又
∵∠ECF=30°,
∴∠ACF+∠ECA=∠FCB+∠ACF=30°,
∴∠ECA=∠FCB,
∴△EMC∽△FBC,
∴$\frac{CM}{BC}$=$\frac{EC}{CF}$.
∵DC=AB=4$\sqrt{3}$,DE=$\frac{1}{2}$AD=2$\sqrt{3}$,∠HED=30°,
∴HD=$\sqrt{3}$,HE=3,
∴在Rt△CHE中,CE=　$\sqrt{CH²+HE²}$=$\sqrt{(5\sqrt{3})²+3²}$=2$\sqrt{21}$，又
∵AM=$\frac{AE}{\sqrt{3}}$=$\frac{2\sqrt{3}}{\sqrt{3}}$=2,AC=$\sqrt{3}$CD=$\sqrt{3}$×4$\sqrt{3}$=12,
∴CM=AC−AM=12−2=10,
∴$\frac{10}{4\sqrt{3}}$=$\frac{2\sqrt{21}}{CF}$，
∴CF=$\frac{12\sqrt{7}}{5}$.
(3)解:如图2,连接AC,过点G作GO⊥AC交AC于点O,交DC于点M,交FC于点N,连接AM.

∵AB:BC=4:3,
∴设AB=4k,BC=3k,
∴AC=5k.在Rt△CBG中,CG²=BC²+BG²,
∵AG=CG,
∴CG²=(3k)²+(4k−CG)²,解得CG=$\frac{25}{8}$k=AG,
∴BG=AB−AG=$\frac{7}{8}$k.
∵AG=CG,GO⊥AC,
∴∠AOG=∠COG=90°,∠AGO=∠OGC=$\frac{1}{2}$∠AGC.
∵∠ECF+$\frac{1}{2}$∠AGC=90°,
∴∠ECF+∠OGC=90°.
∵∠OCG+∠OGC=90°,
∴∠ECF=∠OCG;
∵AB//CD,
∴∠CMG=∠AGO=∠OGC,
∴CM=CG,
∴CM//AG,
∴四边形AMCG为菱形，
∴AO=$\frac{1}{2}$AC=$\frac{5}{2}$k,OG=　$\sqrt{AG^2−AO²}$=$\frac{15}{8}$k.
∵$\frac{AF}{GF}$=n,
∴$\frac{GN}{MN}$=$\frac{GF}{CM}$=$\frac{GF}{AG}$=$\frac{1}{n+1}$,
∴GN=$\frac{1}{n+2}$GM=$\frac{1}{n+2}$.2OG=$\frac{1}{n+2}$×$\frac{15}{4}$k =$\frac{15k}{4(n+2)}$.
∵$\frac{AE}{DE}$=n,
∴AE=$\frac{n}{n+1}$AD=$\frac{n}{n+1}$.3k =$\frac{3nk}{n+1}$.在菱形AMCG中，∠CMG=∠NGC.
∵∠D=∠AOM=90°,
∴∠EAC+∠DMO =180°.又∠CMG+∠DMO=180°,
∴∠EAC=∠CMG,
∴∠EAC=∠NGC.又
∵∠ECF=∠OCG,
∴∠ECA=∠NCG,
∴△CNG∽△CEA,
∴$\frac{GN}{AE}$=$\frac{CG}{AC}$=$\frac{5}{8}$,
∴$\frac{15(n+1)}{4(n+2).3n}$=$\frac{5}{8}$,解得n=$\sqrt{2}$(已舍去负值).