第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1. (西川)如图,在直角梯形 $ABCD$ 中,$AD// BC$,$\angle ABC = 90^{\circ}$,$AB = 7$,$AD = 3$,$BC = 4$。$P$ 为 $AB$ 边上的一动点。若 $\triangle PAD$ 与 $\triangle PBC$ 是相似三角形,则满足条件的点 $P$ 的个数是 (
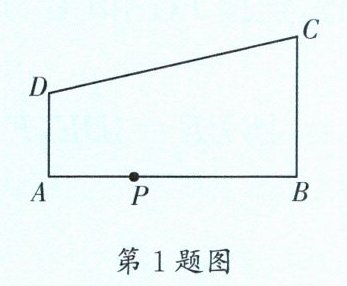
A. 1
B. 2
C. 3
D. 4
B
)
A. 1
B. 2
C. 3
D. 4
答案:
B
2. (成外)如图,在钝角 $\triangle ABC$ 中,$AB = 6\mathrm{cm}$,$AC = 12\mathrm{cm}$,动点 $D$ 从 $A$ 点出发到 $B$ 点停止,动点 $E$ 从 $C$ 点出发到 $A$ 点停止。点 $D$ 运动的速度为 $1\mathrm{cm}/\mathrm{s}$,点 $E$ 运动的速度为 $2\mathrm{cm}/\mathrm{s}$。如果两点同时运动,那么当以 $A$,$D$,$E$ 为顶点的三角形与 $\triangle ABC$ 相似时,运动的时间是
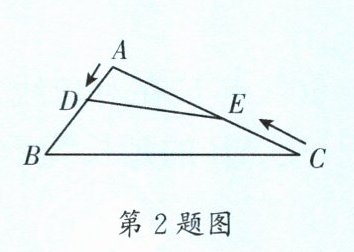
$3s$或$4.8s$
。
答案:
$3s$或$4.8s$
3. (成华区一诊)如图,正方形 $ABCD$ 的边长为 $4$,$AE = EB$,$MN = 2$,线段 $MN$ 的两端在 $CB$,$CD$ 上滑动,当 $CM = $
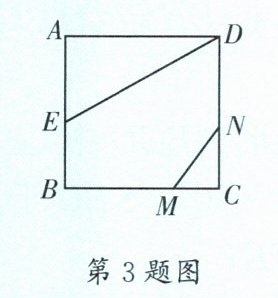
$\frac{4\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$
时,$\triangle ADE$ 与 $\triangle CMN$ 相似。
答案:
$\frac{4\sqrt{5}}{5}$或$\frac{2\sqrt{5}}{5}$
4. (郫都区一诊)如图,在 $\triangle ABC$ 中,$\angle ACB = 90^{\circ}$,$\angle B = 30^{\circ}$,动点 $M$,$N$ 分别在 $BC$,$AB$ 上,且 $AN = 2BM>0$,连接 $AM$,$CN$。若 $AC = 1$,则 $CN + 2AM$ 的最小值为______。
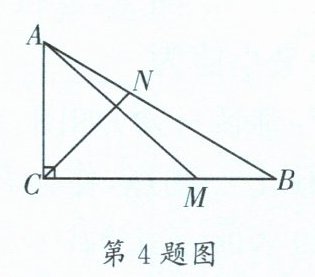

答案:
$\sqrt{17}$
[解析]如图,过点$B$作$BH\perp AB$,且$BH = \frac{1}{2}$,连接$MH$。$\because\angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,$\therefore AB = 2AC = 2$,$\angle CAB = 60^{\circ}$。$\because BH\perp AB$,$\angle ABC = 30^{\circ}$,$\therefore\angle CBH = 60^{\circ} = \angle BAC$。$\because AN = 2BM$,$AC = 1$,$BH = \frac{1}{2}$,$\therefore\frac{BM}{AN}=\frac{BH}{AC}=\frac{1}{2}$,$\therefore\triangle ANC\backsim\triangle BMH$,$\therefore\frac{MH}{CN}=\frac{1}{2}$,$\therefore MH = \frac{1}{2}CN$。$\because CN + 2AM = 2(\frac{1}{2}CN + AM)=2(MH + AM)$,$\therefore$当$A$,$M$,$H$三点共线时,$MH + AM$有最小值,即$CN + 2AM$有最小值,$\therefore CN + 2AM$的最小值$=2\sqrt{AB^{2}+BH^{2}}=2\sqrt{4+\frac{1}{4}}=\sqrt{17}$

$\sqrt{17}$
[解析]如图,过点$B$作$BH\perp AB$,且$BH = \frac{1}{2}$,连接$MH$。$\because\angle ACB = 90^{\circ}$,$\angle ABC = 30^{\circ}$,$\therefore AB = 2AC = 2$,$\angle CAB = 60^{\circ}$。$\because BH\perp AB$,$\angle ABC = 30^{\circ}$,$\therefore\angle CBH = 60^{\circ} = \angle BAC$。$\because AN = 2BM$,$AC = 1$,$BH = \frac{1}{2}$,$\therefore\frac{BM}{AN}=\frac{BH}{AC}=\frac{1}{2}$,$\therefore\triangle ANC\backsim\triangle BMH$,$\therefore\frac{MH}{CN}=\frac{1}{2}$,$\therefore MH = \frac{1}{2}CN$。$\because CN + 2AM = 2(\frac{1}{2}CN + AM)=2(MH + AM)$,$\therefore$当$A$,$M$,$H$三点共线时,$MH + AM$有最小值,即$CN + 2AM$有最小值,$\therefore CN + 2AM$的最小值$=2\sqrt{AB^{2}+BH^{2}}=2\sqrt{4+\frac{1}{4}}=\sqrt{17}$

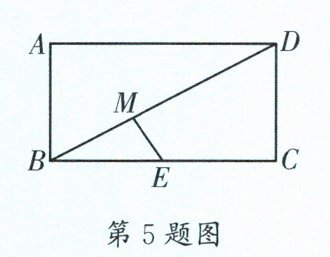
5. (天府新区一诊)如图,在矩形 $ABCD$ 中,$AB = 2$,$BC = 4$,$E$ 为 $BC$ 的中点,连接 $BD$。若 $M$ 是线段 $BD$ 上一动点,则 $EM + \frac{\sqrt{5}}{5}BM$ 的最小值为______。

答案:
$\frac{8}{5}$
[解析]如图,作点$E$关于$BD$的对称点$E'$,连接$BE'$,延长$BE'$交$AD$于点$T$,连接$ME'$,过点$E'$作$E'H'\perp BC$于点$H'$,过点$M$作$MH\perp BC$于点$H$。$\because$四边形$ABCD$是矩形,$\therefore AB = CD = 2$,$BC = AD = 4$,$\angle A = \angle C = 90^{\circ}$,$\therefore BD=\sqrt{BC^{2}+CD^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。$\because MH\perp BC$,$\therefore\angle MHB=\angle C = 90^{\circ}$,$\therefore MH// CD$,$\therefore\triangle BMH\backsim\triangle BDC$,$\therefore\frac{MH}{BM}=\frac{CD}{BD}=\frac{\sqrt{5}}{5}$,$\therefore MH=\frac{\sqrt{5}}{5}BM$。$\because$点$E$,$E'$关于$BD$对称,$\therefore BE = BE' = 2$,$ME = ME'$,$\therefore EM+\frac{\sqrt{5}}{5}BM = E'M + MH\geq E'H'$,$\therefore EM+\frac{\sqrt{5}}{5}BM$的最小值为线段$E'H'$的长。$\because AD// CB$,$\therefore\angle ADB=\angle CBD$。$\because\angle DBE=\angle DBE'$,$\therefore\angle TBD=\angle TDB$,$\therefore TB = TD$。设$TB = TD = x$,$\because\angle A = 90^{\circ}$,$\therefore BT^{2}=AT^{2}+AB^{2}$,即$x^{2}=(4 - x)^{2}+2^{2}$,解得$x=\frac{5}{2}$,$\therefore BT=\frac{5}{2}$,$AT = 4-\frac{5}{2}=\frac{3}{2}$。$\because AD// BC$,$\therefore\angle ATB=\angle H'BE'$。又$\angle A=\angle BH'E' = 90^{\circ}$,$\therefore\triangle ATB\backsim\triangle H'BE'$,$\therefore\frac{E'H'}{BE'}=\frac{AB}{BT}$,$\therefore\frac{E'H'}{2}=\frac{2}{\frac{5}{2}}$,$\therefore E'H'=\frac{8}{5}$,$\therefore EM+\frac{\sqrt{5}}{5}BM$的最小值为$\frac{8}{5}$。

$\frac{8}{5}$
[解析]如图,作点$E$关于$BD$的对称点$E'$,连接$BE'$,延长$BE'$交$AD$于点$T$,连接$ME'$,过点$E'$作$E'H'\perp BC$于点$H'$,过点$M$作$MH\perp BC$于点$H$。$\because$四边形$ABCD$是矩形,$\therefore AB = CD = 2$,$BC = AD = 4$,$\angle A = \angle C = 90^{\circ}$,$\therefore BD=\sqrt{BC^{2}+CD^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}$。$\because MH\perp BC$,$\therefore\angle MHB=\angle C = 90^{\circ}$,$\therefore MH// CD$,$\therefore\triangle BMH\backsim\triangle BDC$,$\therefore\frac{MH}{BM}=\frac{CD}{BD}=\frac{\sqrt{5}}{5}$,$\therefore MH=\frac{\sqrt{5}}{5}BM$。$\because$点$E$,$E'$关于$BD$对称,$\therefore BE = BE' = 2$,$ME = ME'$,$\therefore EM+\frac{\sqrt{5}}{5}BM = E'M + MH\geq E'H'$,$\therefore EM+\frac{\sqrt{5}}{5}BM$的最小值为线段$E'H'$的长。$\because AD// CB$,$\therefore\angle ADB=\angle CBD$。$\because\angle DBE=\angle DBE'$,$\therefore\angle TBD=\angle TDB$,$\therefore TB = TD$。设$TB = TD = x$,$\because\angle A = 90^{\circ}$,$\therefore BT^{2}=AT^{2}+AB^{2}$,即$x^{2}=(4 - x)^{2}+2^{2}$,解得$x=\frac{5}{2}$,$\therefore BT=\frac{5}{2}$,$AT = 4-\frac{5}{2}=\frac{3}{2}$。$\because AD// BC$,$\therefore\angle ATB=\angle H'BE'$。又$\angle A=\angle BH'E' = 90^{\circ}$,$\therefore\triangle ATB\backsim\triangle H'BE'$,$\therefore\frac{E'H'}{BE'}=\frac{AB}{BT}$,$\therefore\frac{E'H'}{2}=\frac{2}{\frac{5}{2}}$,$\therefore E'H'=\frac{8}{5}$,$\therefore EM+\frac{\sqrt{5}}{5}BM$的最小值为$\frac{8}{5}$。

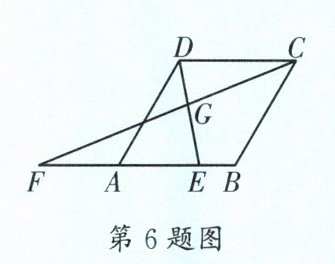
6. (树德实验)如图,在菱形 $ABCD$ 中,$\angle DAB = 60^{\circ}$,$AB = 2$,$E$ 为边 $AB$ 上一个动点,延长 $BA$ 到点 $F$,使 $AF = AE$,且 $CF$,$DE$ 相交于点 $G$。当点 $E$ 从点 $A$ 开始向右运动到点 $B$ 时,点 $G$ 运动路径的长度为______。

答案:
$\frac{2\sqrt{7}}{3}$
[解析]如图1,连接$AG$,延长$AG$交$CD$于点$W$。$\because CD// BF$,$\therefore\frac{FA}{CW}=\frac{AG}{GW}$,$\frac{AG}{GW}=\frac{AE}{DW}$,$\therefore\frac{FA}{CW}=\frac{AE}{DW}$。$\because AF = AE$,$\therefore DW = CW$,$\therefore$点$G$在$AW$上运动。如图2,当点$E$运动到点$B$时,过点$G$作$GH\perp AB$于点$H$,则点$G$的运动路径长即为线段$AG$的长。$\because$四边形$ABCD$为菱形,$\angle DAB = 60^{\circ}$,$AB = 2$,$\therefore CD// BF$,$BD = 2$,$\therefore\triangle CDG\backsim\triangle FBG$,$\therefore\frac{CD}{BF}=\frac{DG}{BG}=\frac{1}{2}$,即$BG = 2DG$。$\because BG + DG = BD = 2$,$\therefore BG=\frac{4}{3}$。在$Rt\triangle GHB$中,$\angle DBA = 60^{\circ}$,$\therefore\angle BGH = 30^{\circ}$,$\therefore BH=\frac{1}{2}BG=\frac{2}{3}$,$\therefore GH=\sqrt{BG^{2}-BH^{2}}=\frac{2\sqrt{3}}{3}$。在$Rt\triangle AHG$中,$AH = 2-\frac{2}{3}=\frac{4}{3}$,$\therefore AG^{2}=(\frac{4}{3})^{2}+(\frac{2\sqrt{3}}{3})^{2}=\frac{28}{9}$,$\therefore AG=\frac{2\sqrt{7}}{3}$,$\therefore$点$G$运动路径的长度为$\frac{2\sqrt{7}}{3}$。


$\frac{2\sqrt{7}}{3}$
[解析]如图1,连接$AG$,延长$AG$交$CD$于点$W$。$\because CD// BF$,$\therefore\frac{FA}{CW}=\frac{AG}{GW}$,$\frac{AG}{GW}=\frac{AE}{DW}$,$\therefore\frac{FA}{CW}=\frac{AE}{DW}$。$\because AF = AE$,$\therefore DW = CW$,$\therefore$点$G$在$AW$上运动。如图2,当点$E$运动到点$B$时,过点$G$作$GH\perp AB$于点$H$,则点$G$的运动路径长即为线段$AG$的长。$\because$四边形$ABCD$为菱形,$\angle DAB = 60^{\circ}$,$AB = 2$,$\therefore CD// BF$,$BD = 2$,$\therefore\triangle CDG\backsim\triangle FBG$,$\therefore\frac{CD}{BF}=\frac{DG}{BG}=\frac{1}{2}$,即$BG = 2DG$。$\because BG + DG = BD = 2$,$\therefore BG=\frac{4}{3}$。在$Rt\triangle GHB$中,$\angle DBA = 60^{\circ}$,$\therefore\angle BGH = 30^{\circ}$,$\therefore BH=\frac{1}{2}BG=\frac{2}{3}$,$\therefore GH=\sqrt{BG^{2}-BH^{2}}=\frac{2\sqrt{3}}{3}$。在$Rt\triangle AHG$中,$AH = 2-\frac{2}{3}=\frac{4}{3}$,$\therefore AG^{2}=(\frac{4}{3})^{2}+(\frac{2\sqrt{3}}{3})^{2}=\frac{28}{9}$,$\therefore AG=\frac{2\sqrt{7}}{3}$,$\therefore$点$G$运动路径的长度为$\frac{2\sqrt{7}}{3}$。


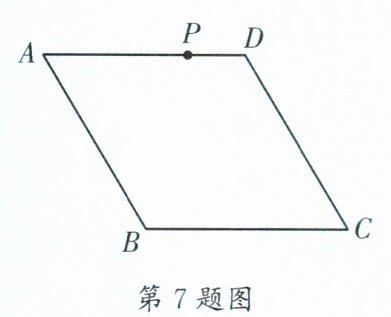
7. (高新区一诊)如图,在菱形 $ABCD$ 中,$AB = 6$,$\angle A = 60^{\circ}$,$P$ 是 $AD$ 边上一动点,将线段 $BC$ 绕点 $P$ 顺时针旋转 $90^{\circ}$ 得到线段 $MN$(点 $B$ 的对应点为点 $M$),当点 $A$ 与点 $M$ 的距离最小时,$\triangle AMN$ 的面积为______。

答案:
$\frac{9\sqrt{3}-9}{2}$
[解析]如图,以$A$为原点,$AD$所在的直线为$x$轴建立直角坐标系,过点$B$作$BG\perp AD$于点$G$,设$MN$交$DA$的延长线于点$H$。设$P(x,0)$,则$AP = x$。$\because\angle BAD = 60^{\circ}$,$\therefore\angle ABG = 30^{\circ}$,$\therefore AG=\frac{1}{2}AB = 3$。由勾股定理,易知$BG = 3\sqrt{3}$,$\therefore PG = AP - AG = x - 3$。$\because$将线段$BC$绕点$P$顺时针旋转$90^{\circ}$得到线段$MN$(点$B$的对应点为点$M$),$\therefore MN\perp BC$,$PB = PM$,$\angle BPM = 90^{\circ}$,$MN = BC = 6$。$\because$四边形$ABCD$为菱形,$\therefore AD// BC$,$\therefore MN\perp AD$,$\angle MPH = 90^{\circ}-\angle BPG=\angle PBG$,$\therefore\angle MHP = 90^{\circ}=\angle PGB$,$\therefore\triangle BGP\cong\triangle PHM(AAS)$,$\therefore MH = PG = x - 3$,$PH = BG = 3\sqrt{3}$,$\therefore AH = PH - AP = 3\sqrt{3}-x$,$\therefore M(x - 3\sqrt{3},x - 3)$,$\therefore AM=\sqrt{(x - 3\sqrt{3})^{2}+(x - 3)^{2}}=\sqrt{2(x-\frac{3\sqrt{3}+3}{2})^{2}+18 - 9\sqrt{3}}$,$\therefore$当$x=\frac{3\sqrt{3}+3}{2}$时,$AM$取最小值,此时点$M(\frac{3 - 3\sqrt{3}}{2},\frac{3\sqrt{3}-3}{2})$,$\therefore AH=\frac{3\sqrt{3}-3}{2}$,$\therefore S_{\triangle AMN}=\frac{1}{2}AH\cdot MN=\frac{1}{2}\times\frac{3\sqrt{3}-3}{2}\times6=\frac{9\sqrt{3}-9}{2}$。

$\frac{9\sqrt{3}-9}{2}$
[解析]如图,以$A$为原点,$AD$所在的直线为$x$轴建立直角坐标系,过点$B$作$BG\perp AD$于点$G$,设$MN$交$DA$的延长线于点$H$。设$P(x,0)$,则$AP = x$。$\because\angle BAD = 60^{\circ}$,$\therefore\angle ABG = 30^{\circ}$,$\therefore AG=\frac{1}{2}AB = 3$。由勾股定理,易知$BG = 3\sqrt{3}$,$\therefore PG = AP - AG = x - 3$。$\because$将线段$BC$绕点$P$顺时针旋转$90^{\circ}$得到线段$MN$(点$B$的对应点为点$M$),$\therefore MN\perp BC$,$PB = PM$,$\angle BPM = 90^{\circ}$,$MN = BC = 6$。$\because$四边形$ABCD$为菱形,$\therefore AD// BC$,$\therefore MN\perp AD$,$\angle MPH = 90^{\circ}-\angle BPG=\angle PBG$,$\therefore\angle MHP = 90^{\circ}=\angle PGB$,$\therefore\triangle BGP\cong\triangle PHM(AAS)$,$\therefore MH = PG = x - 3$,$PH = BG = 3\sqrt{3}$,$\therefore AH = PH - AP = 3\sqrt{3}-x$,$\therefore M(x - 3\sqrt{3},x - 3)$,$\therefore AM=\sqrt{(x - 3\sqrt{3})^{2}+(x - 3)^{2}}=\sqrt{2(x-\frac{3\sqrt{3}+3}{2})^{2}+18 - 9\sqrt{3}}$,$\therefore$当$x=\frac{3\sqrt{3}+3}{2}$时,$AM$取最小值,此时点$M(\frac{3 - 3\sqrt{3}}{2},\frac{3\sqrt{3}-3}{2})$,$\therefore AH=\frac{3\sqrt{3}-3}{2}$,$\therefore S_{\triangle AMN}=\frac{1}{2}AH\cdot MN=\frac{1}{2}\times\frac{3\sqrt{3}-3}{2}\times6=\frac{9\sqrt{3}-9}{2}$。

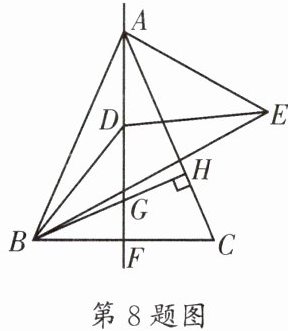
8. (石室联中)如图,在 $\triangle ABC$ 中,$AB = AC = 4$,$AF\perp BC$ 于点 $F$,$BH\perp AC$ 于点 $H$,交 $AF$ 于点 $G$,点 $D$ 在直线 $AF$ 上运动,$BD = DE$,$\angle BDE = 135^{\circ}$,$\angle ABH = 45^{\circ}$,当 $AE$ 取最小值时,$BE$ 的长为______。

答案:
$2\sqrt{6}$
[解析]如图,连接$CG$,$CE$,并延长$EC$,$CE$。$\because BH\perp AC$,$\therefore\angle BHA = 90^{\circ}$。$\because\angle ABH = 45^{\circ}$,$\therefore\angle BAC = 45^{\circ}$。$\because AB = AC$,$AF\perp BC$,$\therefore\angle BAF=\angle CAF = 22.5^{\circ}$,$BF = CF$,$\angle ACB = 67.5^{\circ}$,$\therefore GB = GC$,$\therefore\angle BGF=\angle CGF = 67.5^{\circ}$,$\therefore\angle GBF=\angle GCF = 22.5^{\circ}$。$\because DB = DE$,$\angle BDE = 135^{\circ}$,$\therefore\angle DBE=\angle DEB = 22.5^{\circ}$,$\therefore\angle DBE=\angle GBC=\angle DEB=\angle GCF$,$\therefore\triangle DBE\backsim\triangle GBC$,$\therefore\frac{BD}{BG}=\frac{BE}{BC}$,$\therefore\frac{BD}{BE}=\frac{BG}{BC}$。由题易得$\angle DBG=\angle EBC$,$\therefore\triangle DBG\backsim\triangle EBC$,$\therefore\angle BGD=\angle BCE = 112.5^{\circ}$。$\because\angle ACB = 67.5^{\circ}$,$\therefore\angle ACE = 45^{\circ}$,$\therefore$点$E$的运动轨迹是直线$EC$,$\therefore$当$AE\perp CE$时,$AE$的值最小。由勾股定理,易知最小值为$2\sqrt{2}$,此时$\angle BAE = 90^{\circ}$,$BE=\sqrt{AB^{2}+AE^{2}}=\sqrt{4^{2}+(2\sqrt{2})^{2}}=2\sqrt{6}$。

$2\sqrt{6}$
[解析]如图,连接$CG$,$CE$,并延长$EC$,$CE$。$\because BH\perp AC$,$\therefore\angle BHA = 90^{\circ}$。$\because\angle ABH = 45^{\circ}$,$\therefore\angle BAC = 45^{\circ}$。$\because AB = AC$,$AF\perp BC$,$\therefore\angle BAF=\angle CAF = 22.5^{\circ}$,$BF = CF$,$\angle ACB = 67.5^{\circ}$,$\therefore GB = GC$,$\therefore\angle BGF=\angle CGF = 67.5^{\circ}$,$\therefore\angle GBF=\angle GCF = 22.5^{\circ}$。$\because DB = DE$,$\angle BDE = 135^{\circ}$,$\therefore\angle DBE=\angle DEB = 22.5^{\circ}$,$\therefore\angle DBE=\angle GBC=\angle DEB=\angle GCF$,$\therefore\triangle DBE\backsim\triangle GBC$,$\therefore\frac{BD}{BG}=\frac{BE}{BC}$,$\therefore\frac{BD}{BE}=\frac{BG}{BC}$。由题易得$\angle DBG=\angle EBC$,$\therefore\triangle DBG\backsim\triangle EBC$,$\therefore\angle BGD=\angle BCE = 112.5^{\circ}$。$\because\angle ACB = 67.5^{\circ}$,$\therefore\angle ACE = 45^{\circ}$,$\therefore$点$E$的运动轨迹是直线$EC$,$\therefore$当$AE\perp CE$时,$AE$的值最小。由勾股定理,易知最小值为$2\sqrt{2}$,此时$\angle BAE = 90^{\circ}$,$BE=\sqrt{AB^{2}+AE^{2}}=\sqrt{4^{2}+(2\sqrt{2})^{2}}=2\sqrt{6}$。

查看更多完整答案,请扫码查看


