第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
6. (石室联中)小曼和她的同学组成了“爱琢磨”学习小组,有一次,她们碰到这样一道题:“已知正方形ABCD,点E,F,G,H分别在边AB,BC,CD,DA上,若$EG⊥FH$,则$\frac {EG}{FH}= 1$。”为了解决这个问题,经过思考,大家给出了以下两个方案:
方案一:过点A作$AM// HF$交BC于点M,过点B作$BN// EG$交CD于点N;
方案二:过点H作$HM⊥BC$交BC于点M,过点E作$EN⊥CD$交CD于点N。
(1)对小曼遇到的问题,请在甲、乙两个方案中任选一个加以证明(如图1);
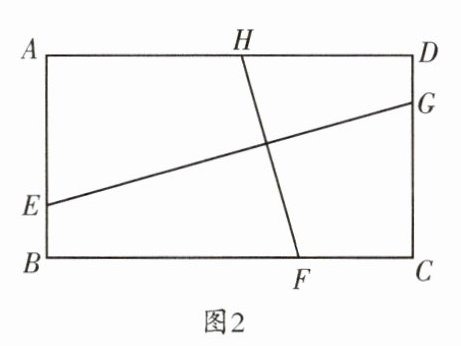
(2)如果把条件中的“正方形”改为“矩形”(如图2),并设$AB= 3$,$BC= 5$,求$\frac {EG}{FH}$的值;
(3)如图3,在四边形ABCD中,$∠ABC= 90^{\circ }$,$AB= AD= 8$,$BC= CD= 4$,点E,F分别在线段AB,BC上,且$AF⊥DE$,求$\frac {DE}{AF}$的值。
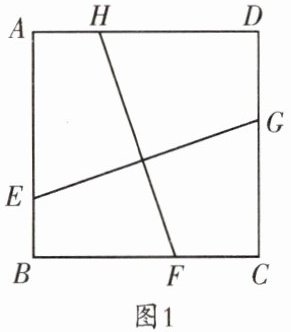

方案一:过点A作$AM// HF$交BC于点M,过点B作$BN// EG$交CD于点N;
方案二:过点H作$HM⊥BC$交BC于点M,过点E作$EN⊥CD$交CD于点N。
(1)对小曼遇到的问题,请在甲、乙两个方案中任选一个加以证明(如图1);
(2)如果把条件中的“正方形”改为“矩形”(如图2),并设$AB= 3$,$BC= 5$,求$\frac {EG}{FH}$的值;
(3)如图3,在四边形ABCD中,$∠ABC= 90^{\circ }$,$AB= AD= 8$,$BC= CD= 4$,点E,F分别在线段AB,BC上,且$AF⊥DE$,求$\frac {DE}{AF}$的值。



答案:
解:
(1)选择方案一.证明如下:
如图1,过点A作AM//HF交BC于点M,过点B作BN//EG交CD于点N,
∴四边形AMFH、四边形BNGE都是平行四边形,
∴AM=HF,BN=EG.
∵EG⊥FH,AM//HF,BN//EG,
∴AM⊥BN,
∴∠BAM=90°−∠ABN=∠CBN.
∵四边形ABCD为正方形,
∴AB=BC,∠ABM=∠BCN=90°,
∴△ABM≌△BCN (ASA),
∴AM=BN,
∴EG=FH,
∴EG/FH=1.


选择方案二.证明如下:
如图2,过点H作HM⊥BC交BC于点M,过点E作EN⊥CD交CD于点N,
∴四边形ABMH、四边形BCNE都是矩形,
∴AB=HM,BC=EN,BC//EN,
∴∠1=∠MFH.
∵AB=BC,
∴HM=EN.
∵EG⊥FH,
∴∠1+∠GEN=90°.
∵EN⊥CD,
∴∠GEN+∠EGN=90°,
∴∠1=∠MFH=∠EGN;
∵∠HMF=∠ENG=90°,HM=EN,
∴△HMF≌△ENG(AAS),
∴FH=EG,
∴EG/FH=1.
(2)如图3,过点A作AM//HF交BC于点M,作AN//EG交CD的延长线于点N,易得AM=HF,AN=EG.
∵四边形ABCD是矩形,
∴∠BAD=∠ADN =∠ABM=90°.
∵EG⊥FH,AM//HF,AN//EG,
∴AM⊥AN,
∴∠NAM=90°,
∴∠BAM=∠DAN,
∴△ABM∽△ADN,
∴AM/AN=AB/AD.
∵AB=3,AD=BC=5,
∴EG/FH=AN/AM=AD/AB=5/3.


(3)如图4,过点D作MN⊥BC,交BC的延长线于点M,过点A作AN⊥MN于点N,连接AC;
∵∠ABC=90°,AN⊥MN,MN⊥BC,
∴四边形ABMN是矩形,
∴∠N=∠M=90°,AN=BM,MN=AB=8.
∵AD=AB,CD=BC,AC=AC,
∴△ACD≌△ACB(SSS),
∴∠ADC=∠ABC=90°,
∴∠ADN+∠CDM=90°.又
∵∠ADN+∠DAN=90°,
∴∠DAN =∠CDM.
∵∠N=∠M=90°,
∴△ADN∽△DCM,
∴DM/AN=CM/DN=CD/AD=4/8=1/2,
∴AN=2DM,DN=2CM.
∵DC²=CM²+DM²,
∴16=CM²+(8−2CM)²,解得CM=4(不合题意,舍去)或CM=12/5,
∴BM=BC+CM=32/5=AN.过点E作EG⊥MN于点G,过点F作FH⊥AN 于点H.同
(1)易得∠AFH=∠DEG.又
∵∠AHF=∠DGE=90°,
∴△DEG∽△AFH,
∴DE/AF=EG/HF.
∵EG=AN=32/5,HF=AB=8,
∴DE/AF=(32/5)/8=4/5.
解:
(1)选择方案一.证明如下:
如图1,过点A作AM//HF交BC于点M,过点B作BN//EG交CD于点N,
∴四边形AMFH、四边形BNGE都是平行四边形,
∴AM=HF,BN=EG.
∵EG⊥FH,AM//HF,BN//EG,
∴AM⊥BN,
∴∠BAM=90°−∠ABN=∠CBN.
∵四边形ABCD为正方形,
∴AB=BC,∠ABM=∠BCN=90°,
∴△ABM≌△BCN (ASA),
∴AM=BN,
∴EG=FH,
∴EG/FH=1.


选择方案二.证明如下:
如图2,过点H作HM⊥BC交BC于点M,过点E作EN⊥CD交CD于点N,
∴四边形ABMH、四边形BCNE都是矩形,
∴AB=HM,BC=EN,BC//EN,
∴∠1=∠MFH.
∵AB=BC,
∴HM=EN.
∵EG⊥FH,
∴∠1+∠GEN=90°.
∵EN⊥CD,
∴∠GEN+∠EGN=90°,
∴∠1=∠MFH=∠EGN;
∵∠HMF=∠ENG=90°,HM=EN,
∴△HMF≌△ENG(AAS),
∴FH=EG,
∴EG/FH=1.
(2)如图3,过点A作AM//HF交BC于点M,作AN//EG交CD的延长线于点N,易得AM=HF,AN=EG.
∵四边形ABCD是矩形,
∴∠BAD=∠ADN =∠ABM=90°.
∵EG⊥FH,AM//HF,AN//EG,
∴AM⊥AN,
∴∠NAM=90°,
∴∠BAM=∠DAN,
∴△ABM∽△ADN,
∴AM/AN=AB/AD.
∵AB=3,AD=BC=5,
∴EG/FH=AN/AM=AD/AB=5/3.


(3)如图4,过点D作MN⊥BC,交BC的延长线于点M,过点A作AN⊥MN于点N,连接AC;
∵∠ABC=90°,AN⊥MN,MN⊥BC,
∴四边形ABMN是矩形,
∴∠N=∠M=90°,AN=BM,MN=AB=8.
∵AD=AB,CD=BC,AC=AC,
∴△ACD≌△ACB(SSS),
∴∠ADC=∠ABC=90°,
∴∠ADN+∠CDM=90°.又
∵∠ADN+∠DAN=90°,
∴∠DAN =∠CDM.
∵∠N=∠M=90°,
∴△ADN∽△DCM,
∴DM/AN=CM/DN=CD/AD=4/8=1/2,
∴AN=2DM,DN=2CM.
∵DC²=CM²+DM²,
∴16=CM²+(8−2CM)²,解得CM=4(不合题意,舍去)或CM=12/5,
∴BM=BC+CM=32/5=AN.过点E作EG⊥MN于点G,过点F作FH⊥AN 于点H.同
(1)易得∠AFH=∠DEG.又
∵∠AHF=∠DGE=90°,
∴△DEG∽△AFH,
∴DE/AF=EG/HF.
∵EG=AN=32/5,HF=AB=8,
∴DE/AF=(32/5)/8=4/5.
查看更多完整答案,请扫码查看


