第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
1.(武侯区一诊)在矩形ABCD中,$\frac {AD}{AB}= k$,在射线AD上取一点E,连接CE,且满足$AE= CE$,直线BD与直线CE相交于点F.
【尝试初探】(1)如图1,当$k>1$时,若$EF= 1,CF= 4$,求线段DE的长;
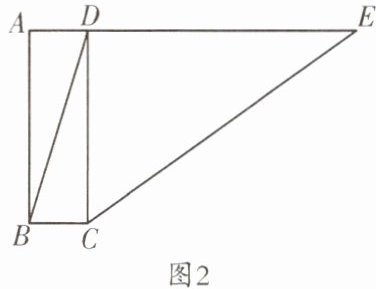
【深入探究】(2)如图2,当$k<1$时,若$\frac {BD}{CE}= \frac {3}{5}$,求k的值;
【拓展延伸】(3)若$DE= DF$,试探究线段EF与线段CF之间满足的数量关系.
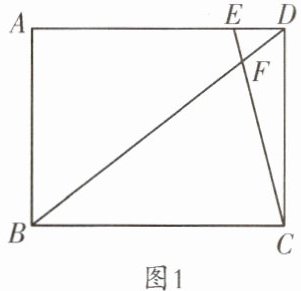
【尝试初探】(1)如图1,当$k>1$时,若$EF= 1,CF= 4$,求线段DE的长;
【深入探究】(2)如图2,当$k<1$时,若$\frac {BD}{CE}= \frac {3}{5}$,求k的值;
【拓展延伸】(3)若$DE= DF$,试探究线段EF与线段CF之间满足的数量关系.


答案:
解:
(1)
∵四边形ABCD是矩形,
∴AD//BC,
∴∠EDF = ∠FBC,∠DEF = ∠FCB,
∴△EFD∽△CFB,
∴$\frac{EF}{CF}$=$\frac{ED}{BC}$.
∵EF = 1,CF = 4,
∴$\frac{EF}{CF}$=$\frac{1}{4}$.
设ED = x,则BC = AD = 4x.
∵AE = CE = 5,DE = AD - AE,
∴x = 4x - 5,解得$x=\frac{5}{3}$,即ED=$\frac{5}{3}$.
(2)
∵$\frac{BD}{CE}$=$\frac{3}{5}$,
∴设DE = x,BD = 3a,则CE = 5a,
∴AD = 5a - x.
在Rt△BCD和Rt△CDE中,$BD^{2}-BC^{2} = CE^{2}-DE^{2}$,即$9a^{2}-(5a - x)^{2}=25a^{2}-x^{2}$,解得$x=\frac{41}{10}a$,
∴AD = 5a - x=$\frac{9}{10}a$,
∴$AD^{2} = \frac{81a^{2}}{100}$,
∴$AB^{2}=9a^{2}-\frac{81a^{2}}{100}=\frac{819}{100}a^{2}$,
∴$\frac{AD^{2}}{AB^{2}} = \frac{81}{819}=k^{2}$,
∴$k=\sqrt{\frac{81}{819}}=\frac{3\sqrt{91}}{91}$.
(3)①当k > 1时,如题图1,设DE = a,BC = b.
∵DE = DF = a,∠DEF = ∠DFE = ∠BFC = ∠BCF,
∴BC = BF = b,EC = AE = b - a.
∵$BD^{2}-BC^{2}=EC^{2}-ED^{2}=CD^{2}$,即$(a + b)^{2}-b^{2}=(b - a)^{2}-a^{2}$,整理得$a^{2}+4ab - b^{2}=0$,
∴$a=-2b\pm \sqrt {5}b$.
∵a > 0,b > 0,
∴$a=(\sqrt {5}-2)b$,
∴$\frac{EF}{FC}$=$\frac{DE}{BC} = \frac{a}{b}=\sqrt {5}-2$.
②当k < 1时,如图,延长DB,EC交于点F.设DE = m,CE = n.

∵AE = CE,
∴AD = n - m.
∵DE = DF = m,
∴∠F = ∠E.
∵DE//BC,
∴∠BCF = ∠F = ∠E,
∴BF = BC = AD = n - m,BD = DF - BF = 2m - n.
∵$BD^{2}-BC^{2}=EC^{2}-ED^{2}=CD^{2}$,
∴$(2m - n)^{2}-(n - m)^{2}=n^{2}-m^{2}$,整理得$n^{2}+2mn - 4m^{2}=0$,
∴$n=-m\pm \sqrt {5}m$.
∵m > 0,n > 0,
∴$n=(\sqrt {5}-1)m$,
∴$\frac{EF}{CF}$=$\frac{DE}{BC} = \frac{m}{n - m}=\sqrt {5}+2$.
综上所述,$EF=(\sqrt {5}\pm 2)CF$.
解:
(1)
∵四边形ABCD是矩形,
∴AD//BC,
∴∠EDF = ∠FBC,∠DEF = ∠FCB,
∴△EFD∽△CFB,
∴$\frac{EF}{CF}$=$\frac{ED}{BC}$.
∵EF = 1,CF = 4,
∴$\frac{EF}{CF}$=$\frac{1}{4}$.
设ED = x,则BC = AD = 4x.
∵AE = CE = 5,DE = AD - AE,
∴x = 4x - 5,解得$x=\frac{5}{3}$,即ED=$\frac{5}{3}$.
(2)
∵$\frac{BD}{CE}$=$\frac{3}{5}$,
∴设DE = x,BD = 3a,则CE = 5a,
∴AD = 5a - x.
在Rt△BCD和Rt△CDE中,$BD^{2}-BC^{2} = CE^{2}-DE^{2}$,即$9a^{2}-(5a - x)^{2}=25a^{2}-x^{2}$,解得$x=\frac{41}{10}a$,
∴AD = 5a - x=$\frac{9}{10}a$,
∴$AD^{2} = \frac{81a^{2}}{100}$,
∴$AB^{2}=9a^{2}-\frac{81a^{2}}{100}=\frac{819}{100}a^{2}$,
∴$\frac{AD^{2}}{AB^{2}} = \frac{81}{819}=k^{2}$,
∴$k=\sqrt{\frac{81}{819}}=\frac{3\sqrt{91}}{91}$.
(3)①当k > 1时,如题图1,设DE = a,BC = b.
∵DE = DF = a,∠DEF = ∠DFE = ∠BFC = ∠BCF,
∴BC = BF = b,EC = AE = b - a.
∵$BD^{2}-BC^{2}=EC^{2}-ED^{2}=CD^{2}$,即$(a + b)^{2}-b^{2}=(b - a)^{2}-a^{2}$,整理得$a^{2}+4ab - b^{2}=0$,
∴$a=-2b\pm \sqrt {5}b$.
∵a > 0,b > 0,
∴$a=(\sqrt {5}-2)b$,
∴$\frac{EF}{FC}$=$\frac{DE}{BC} = \frac{a}{b}=\sqrt {5}-2$.
②当k < 1时,如图,延长DB,EC交于点F.设DE = m,CE = n.

∵AE = CE,
∴AD = n - m.
∵DE = DF = m,
∴∠F = ∠E.
∵DE//BC,
∴∠BCF = ∠F = ∠E,
∴BF = BC = AD = n - m,BD = DF - BF = 2m - n.
∵$BD^{2}-BC^{2}=EC^{2}-ED^{2}=CD^{2}$,
∴$(2m - n)^{2}-(n - m)^{2}=n^{2}-m^{2}$,整理得$n^{2}+2mn - 4m^{2}=0$,
∴$n=-m\pm \sqrt {5}m$.
∵m > 0,n > 0,
∴$n=(\sqrt {5}-1)m$,
∴$\frac{EF}{CF}$=$\frac{DE}{BC} = \frac{m}{n - m}=\sqrt {5}+2$.
综上所述,$EF=(\sqrt {5}\pm 2)CF$.
查看更多完整答案,请扫码查看


