《2025年名校题库九年级数学全一册北师大版》

1. (锦江区期末)如图,在$10×6$的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形。E是格点四边形ABCD的AB边上的一动点,连接ED,EC。若格点$△DAE与△EBC$相似,则$DE+EC$的长为 (3√13或5√5)

A. $3\sqrt {13}$
B. $\sqrt {149}$
C. $3\sqrt {13}或5\sqrt {5}$
D. $3\sqrt {13}或\sqrt {149}$

答案： C [解析]设AE=x,则EB=8−x.根据勾股定理可得DE=√AD²+AE²=√3²+x²=√9+x²,EC=√BC²+BE²=√4²+(8−x)²=√16+(8−x)².格点△DAE与△EBC相似,分两种情况:①如果△DAE∽△EBC,那么DE/EC=DA/EB=AE/BC,即DE/EC=3/(8−x)=x/4,解得x1=2,x2=6.当x=2时,DE=√9+2²=√13,EC=√16+(8−2)²=2√13,
∴DE+EC=√13+2√13=3√13;当x=6时,DE=√9+6²=3√5,EC=√16+(8−6)²=2√5,
∴DE+EC=3√5+2√5=5√5.②如果△DAE∽△CBE,那么DE/CE=DA/CB=AE/BE,即DE/CE=3/4=x/(8−x),解得x=24/7.当x=24/7时，DE=√9+(24/7)²=3√113/7,EC=√16+(8 - 24/7)²=4√113/7,
∴DE+EC=3√113/7+4√113/7=√113(不符合题意，舍去).综上所述，DE+EC的长为3√13或5√5.

2. (实外)如图,在矩形ABCD中,$AB= 2$,$BC= 3$。若E是边CD的中点,连接AE,过点B作$BF⊥AE$于点F,则BF的长为3√10/5。

答案： 3√10/5

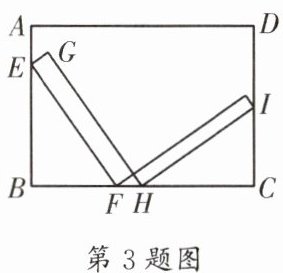
3. (高新区期末)两本完全相同的书侧放在长方体形书柜中,其截面如图所示。已知书的长度EF为20 cm,厚度EG为2 cm。书角F到书柜底部B的距离比书角H到书柜底部C的距离少4 cm,则书角F与书角H的距离FH为____cm。

答案：
2.5 [解析]设BF=xcm,则CH=(x+4)cm.
如图，设两本书的交点为M.
∵EG=2cm,
∴FM=2cm.由题易得，∠EBF=∠FMH=∠ICH=90°,
∴∠BEF=∠MFH=90°−∠BFE,∠MFH=∠CHI=90°−∠MHF,
∴∠BEF=∠CHI.又
∵∠B=∠C=90°,EF=IH,
∴△BEF≌△CHI(AAS),
∴BF=CI=xcm,BE=CH=(x+4)cm.
∵EF=20cm,在Rt△BEF中,BE²+BF²=EF²,
∴(x+4)²+x²=400,解得x=12(负值已舍去),
∴BE=16cm,BF=12cm.
∵∠BEF=∠MFH,∠EBF=∠FMH,
∴△BEF∽△MFH,
∴BE/EF=MF/FH,即16/20=2/FH,解得FH=2.5cm.

4. (武侯区一诊)如图,在正方形ABCD中,点E,F分别在边AB,AD上,$EF⊥CE$于点E。
(1)求证：$△AEF\backsim △BCE$；
证明:∵四边形ABCD为正方形，∴∠A=∠B=90°,∴∠AEF+∠AFE=90°.又∵∠FEC=90°,∴∠AEF+∠CEB=90°,∴∠AFE=∠CEB,∴△AEF∽△BCE.
(2)若$\frac {BE}{AE}= \frac {1}{2}$,求$\frac {EF}{CE}$的值。
解:∵BE/AE=1/2,∴可设BE=x,则AE=2x，AB=3x=BC.∵△AEF∽△BCE,∴EF/CE=AE/BC=2x/3x=$\frac{2}{3}$.

答案：
(1)证明:
∵四边形ABCD为正方形，
∴∠A=∠B=90°,
∴∠AEF+∠AFE=90°.又
∵∠FEC=90°,
∴∠AEF+∠CEB=90°,
∴∠AFE=∠CEB,
∴△AEF∽△BCE.
(2)解:
∵BE/AE=1/2,
∴可设BE=x,则AE=2x，AB=3x=BC.
∵△AEF∽△BCE,
∴EF/CE=AE/BC=2x/3x=2/3.