《2025年名校题库九年级数学全一册北师大版》

1. (青羊区一诊)如图,在正方形 $ABCD$ 中,$E$ 是线段 $CD$ 上一点,连接 $AE$,将 $\triangle ADE$ 沿 $AE$ 翻折至 $\triangle AFE$,连接 $BF$ 并延长交 $AE$ 的延长线于点 $P$。当 $PF= \frac{\sqrt{2}}{2}BF$ 时,$\frac{DE}{CD}= $______。

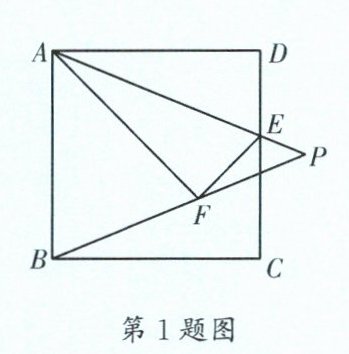
答案：
$\sqrt{2}-1$ 【解析】如图，过点$A$作$AM\perp BP$于点$M$，过点$E$作$EN\perp BP$于点$N$。$\because$ 四边形$ABCD$是正方形，$\therefore AD=AB$，$\angle BAD=90^{\circ}$。 由翻折的性质可知，$AD=AF$，$\angle DAE=\angle EAF$，$\therefore AB=AF$。 $\because AM\perp BF$，$\therefore BM=FM$，$\angle BAM=\angle FAM$，$\therefore \angle PAM=\angle PAF+\angle FAM=\frac{1}{2}\angle BAD=45^{\circ}$。 $\because \angle AMP=90^{\circ}$，$\therefore \angle P=\angle PAM=45^{\circ}$，$\therefore AM=MP$。 设$BF=2a$，则$PF=\frac{\sqrt{2}}{2}BF=\sqrt{2}a$，$BM=MF=a$，$\therefore AM=PM=FM+PF=a+\sqrt{2}a$。 $\because \angle AMF=\angle AFE=\angle ENF=90^{\circ}$，$\therefore \angle AFM+\angle EFN=90^{\circ}$，$\angle EFN+\angle FEN=90^{\circ}$，$\therefore \angle AFM=\angle FEN$，$\therefore \triangle AMF\backsim\triangle FNE$，$\therefore \frac{AM}{FM}=\frac{FN}{EN}=\frac{a+\sqrt{2}a}{a}=1+\sqrt{2}$。 设$EN=PN=x$，则$FN=(1+\sqrt{2})x$，$\therefore (1+\sqrt{2})x+x=\sqrt{2}a$，$\therefore x=(\sqrt{2}-1)a$，$\therefore EN=(\sqrt{2}-1)a$，$\therefore \frac{EF}{AF}=\frac{EN}{FM}=\frac{(\sqrt{2}-1)a}{a}=\sqrt{2}-1$。 $\because CD=AD=AF$，$DE=EF$，$\therefore \frac{DE}{CD}=\frac{EF}{AF}=\sqrt{2}-1$。

2. (树德实验)如图,在 $\triangle ABC$ 中,$D$ 为 $BC$ 上一点,$E$ 为 $AD$ 上一点,$\angle BED= \angle BAC= 2\angle DEC$,若 $\frac{CD}{BD}= \frac{1}{4}$,$BE= 8\sqrt{2}$,则 $AE= $______。

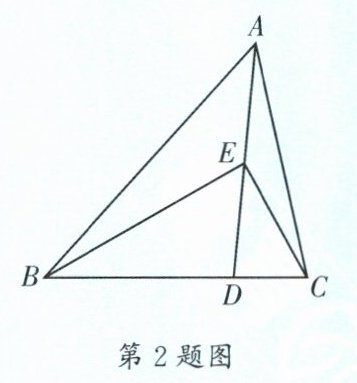
答案：
$\sqrt{34}-\sqrt{2}$ 【解析】如图，过点$C$作$CF\perp AD$于点$F$，过点$B$作$BG\perp AD$，交$AD$的延长线于点$G$，在$AD$上取一点$H$，连接$CH$，使$EH=CH$。$\because BG\perp AD$，$CF\perp AD$，$\therefore BG// CF$，$\therefore \triangle CFD\backsim\triangle BGD$，$\therefore \frac{CF}{BG}=\frac{DF}{DG}=\frac{CD}{BD}=\frac{1}{4}$。$\because EH=CH$，$\therefore \angle HEC=\angle HCE$。$\because \angle FHC=\angle HEC+\angle HCE$，$\therefore \angle FHC=2\angle DEC$。$\because \angle BED=2\angle DEC$，$\therefore \angle BED=\angle FHC$。$\because \angle BGE=\angle CFH=90^{\circ}$，$\therefore \triangle BGE\backsim\triangle CFH$，$\therefore \frac{CH}{BE}=\frac{CF}{BG}=\frac{1}{4}$，$\therefore \frac{CH}{8\sqrt{2}}=\frac{1}{4}$，$\therefore CH=2\sqrt{2}$，$\therefore HE=2\sqrt{2}$。 设$AE=x$，则$AH=x+2\sqrt{2}$。$\because \angle BED=\angle BAC$，$\angle BED=\angle BAE+\angle ABE$，$\angle BAC=\angle BAG+\angle CAF$，$\therefore \angle ABE=\angle CAF$。$\because \angle BED=\angle FHC$，$\therefore \angle AEB=\angle CHA$，$\therefore \triangle ABE\backsim\triangle CAH$，$\therefore \frac{BE}{AH}=\frac{AE}{CH}$，$\therefore \frac{8\sqrt{2}}{x+2\sqrt{2}}=\frac{x}{2\sqrt{2}}$，解得$x=-\sqrt{2}+\sqrt{34}$(负值已舍去)，$\therefore AE=\sqrt{34}-\sqrt{2}$。

3. (青羊区一诊)如图,在矩形 $ABCD$ 中,$AB= 2AD= 8$,$E$,$F$ 分别是边 $AB$,$CD$ 的中点,$P$ 为 $AD$ 边上的一动点,过点 $P$ 作与 $AB$ 平行的直线交 $AF$ 于点 $G$,连接 $PE$,$M$ 是 $PE$ 的中点,连接 $MG$,则 $MG$ 的最小值为______。

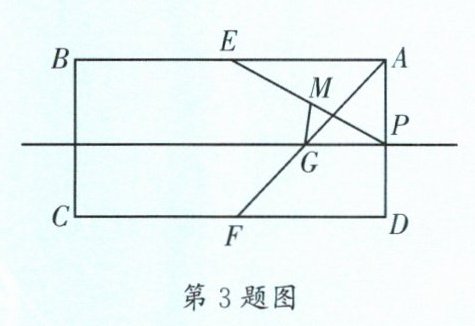
答案：
$\frac{2\sqrt{5}}{5}$ 【解析】如图，以点$D$为原点、直线$CD$为$x$轴、直线$AD$为$y$轴建立平面直角坐标系。$\because$ 四边形$ABCD$是矩形，且$AB=2AD=8$，$\therefore A(0,4)$，$B(-8,4)$，$C(-8,0)$，$D(0,0)$。$\because E$，$F$分别是边$AB$，$CD$的中点，$\therefore E(-4,4)$，$F(-4,0)$。 设$P(0,t)$。$\because M$是$PE$的中点，$\therefore M(-2,\frac{t+4}{2})$。 设直线$AG$的解析式为$y=kx+b$，则$\begin{cases}-4k+b=0\\b=4\end{cases}$，解得$\begin{cases}k=1\\b=4\end{cases}$，$\therefore$ 直线$AG$的解析式为$y=x+4$。$\because PG// x$轴交$AF$于点$G$，$\therefore G(t-4,t)$，$\therefore MG^{2}=[(t-4)-(-2)]^{2}+(t-\frac{t+4}{2})^{2}=\frac{5}{4}t^{2}-6t+8=\frac{5}{4}(t-\frac{12}{5})^{2}+\frac{4}{5}$。$\because \frac{5}{4}＞0$，$\therefore MG^{2}$有最小值为$\frac{4}{5}$。$\because MG＞0$，$\therefore MG$的最小值为$\sqrt{\frac{4}{5}}=\frac{2\sqrt{5}}{5}$。

4. (天府新区一诊)如图,在矩形 $ABCD$ 中,$AB= 4$,$AD= 6$,$E$ 是 $BC$ 上的动点,$F$ 是 $BE$ 的中点,$AE$ 与 $FD$ 交于点 $G$,则 $AG$ 的最小值为______。

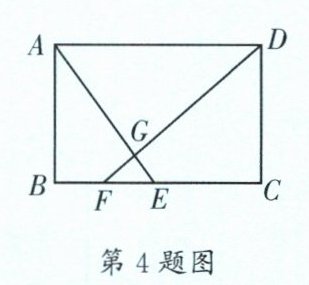
答案：
$\frac{6\sqrt{10}}{5}$ 【解析】如图，过点$G$作$GM\perp AB$于点$M$，$GN\perp BC$于点$N$。 令$MB=x$，$MG=y$，$BF=a$。$\because F$是$BE$的中点，$\therefore FE=BF=a$。$\because$ 四边形$ABCD$是矩形，$\therefore AD=BC=6$，$AB=DC=4$，$AD// BC$，$AB// DC$，$\therefore \triangle AMG\backsim\triangle ABE$，$\therefore \frac{MG}{BE}=\frac{AM}{AB}$。 同理可得$\triangle FGN\backsim\triangle FDC$，$\therefore \frac{GN}{DC}=\frac{FN}{FC}$，$\therefore \frac{y}{2a}=\frac{4-x}{4}$，$\frac{x}{4}=\frac{y-a}{6-a}$，$\therefore y=3x$。在$Rt\triangle AMG$中，$\because AG^{2}=AM^{2}+MG^{2}$，$\therefore AG^{2}=(4-x)^{2}+(3x)^{2}=10x^{2}-8x+16=10(x-\frac{2}{5})^{2}+\frac{72}{5}$，$\therefore$ 当$x=\frac{2}{5}$时，$AG^{2}$有最小值为$\frac{72}{5}$，$\therefore AG$的最小值是$\sqrt{\frac{72}{5}}=\frac{6\sqrt{10}}{5}$。

5. (师大一中)如图,在 $\triangle ABC$ 中,$\angle ACB= 60^{\circ}$,$CD$ 为 $AB$ 边上的高,$P$ 为 $CD$ 上一点,$PQ\perp CD$ 交 $AC$ 于点 $Q$。已知 $CP= 12$,$PD= 3$,连接 $DQ$。若 $\angle PQD= 2\angle ACD$,则 $AB$ 的长为______。

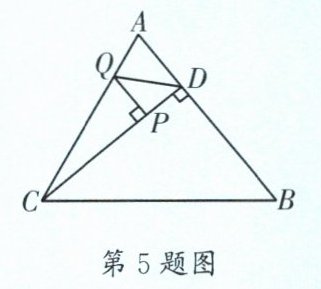
答案：
$25\sqrt{3}-25$ 【解析】如图，过点$C$作$CN\perp DQ$，交$DQ$的延长线于点$N$，过点$B$作$BM\perp AC$于点$M$。$\because PQ\perp CD$，$\therefore \angle N=\angle CPQ=90^{\circ}$，$\therefore \angle NCP+\angle NQP=180^{\circ}$。$\because \angle NQP+\angle PQD=180^{\circ}$，$\therefore \angle NCP=\angle PQD$。$\because \angle PQD=2\angle ACD$，$\therefore \angle NCQ=\angle PCQ$，$\therefore QN=QP$。$\because CQ=CQ$，$\therefore Rt\triangle NCQ\cong Rt\triangle PCQ$(HL)，$\therefore CN=CP=12$。$\because PD=3$，$\therefore CD=3+12=15$，$\therefore ND=\sqrt{CD^{2}-CN^{2}}=\sqrt{15^{2}-12^{2}}=9$。 设$PQ=x$，则$NQ=x$，$DQ=9-x$。在$Rt\triangle QPD$中，由勾股定理得$PQ^{2}+PD^{2}=DQ^{2}$，$\therefore x^{2}+3^{2}=(9-x)^{2}$，解得$x=4$，$\therefore PQ=4$。$\because CD\perp AB$，$\therefore \angle CDB=90^{\circ}$，$\therefore \angle CDB=\angle CMB$。$\because \angle COM=\angle BOD$，$\therefore \angle MCO=\angle OBD$。$\because \angle CPQ=\angle BMA=90^{\circ}$，$\therefore \triangle QPC\backsim\triangle AMB$，$\therefore \frac{QP}{CP}=\frac{AM}{BM}=\frac{4}{12}=\frac{1}{3}$。 设$AM=\sqrt{3}a$，则$BM=3\sqrt{3}a$。在$Rt\triangle CMB$中，$\angle BCM=60^{\circ}$，$\therefore \angle CBM=30^{\circ}$，$\therefore CM=3a$。$\because \angle ADC=\angle QPC=90^{\circ}$，$\angle QCP=\angle ACD$，$\therefore \triangle QCP\backsim\triangle ACD$，$\therefore \frac{QP}{CP}=\frac{AD}{CD}$，即$\frac{4}{12}=\frac{AD}{15}$，$\therefore AD=5$，$\therefore AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{5^{2}+15^{2}}=5\sqrt{10}$，$\therefore \sqrt{3}a+3a=5\sqrt{10}$，解得$a=\frac{5\sqrt{10}}{3+\sqrt{3}}=\frac{15\sqrt{10}-5\sqrt{30}}{6}$，由勾股定理得$AB=\sqrt{AM^{2}+BM^{2}}=\sqrt{(\sqrt{3}a)^{2}+(3\sqrt{3}a)^{2}}=\sqrt{30}a=25\sqrt{3}-25$。

6. (青白江区一诊)如图,在菱形 $ABCD$ 中,$AB= 6$,$E$ 是边 $BC$ 上一点,在 $AE$ 的右侧作 $EF= AE$,且 $\angle AEF= \angle ABC= 120^{\circ}$,连接 $CF$,连接 $AF$ 交 $CD$ 于点 $G$。若 $G$ 为边 $CD$ 的三等分点,则 $BE$ 的长为______。

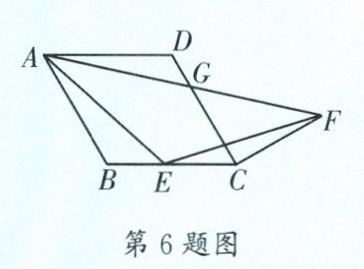
答案：
$\frac{12}{5}$或$\frac{6}{7}$ 【解析】如图1，在$BC$的延长线上取点$P$，使得$\angle FPE=\angle ABC=120^{\circ}$，则$\angle FEP=\angle AEC-\angle AEF=\angle ABC+\angle BAE-\angle AEF=\angle BAE$。 又$\because EF=AE$，$\therefore \triangle EFP\cong\triangle AEB$(AAS)，$\therefore FP=BE$，$EP=AB$。 由$EP=AB=BC$，得$BE=CP$，$\therefore FP=CP$，$\angle FCP=\frac{1}{2}(180^{\circ}-\angle FPE)=30^{\circ}$。在菱形$ABCD$中，$\because AB// CD$，$\therefore \angle DCP=\angle ABC=120^{\circ}$，$\therefore \angle DCF=\angle DCP-\angle FCP=90^{\circ}$。如图2，连接$AC$，$BD$交于点$O$。$\because AB=BC$，$\angle ABC=120^{\circ}$，$\therefore \angle BAO=30^{\circ}$，$\therefore BO=\frac{1}{2}AB$，$\therefore AO=\sqrt{3}BO=\frac{\sqrt{3}}{2}AB$，$\therefore AC=2AO=\sqrt{3}AB$。如图3，过点$A$作$AH\perp CD$交$CD$的延长线于点$H$，$\therefore \angle AHD=\angle DCF=90^{\circ}$，$\therefore AH// CF$，$\therefore \triangle AHG\backsim\triangle FCG$，$\therefore \frac{AH}{CF}=\frac{HG}{CG}$。$\because \angle ADH=60^{\circ}$，$\therefore DH=\frac{1}{2}AD=3$，$\therefore AH=\sqrt{3}DH=3\sqrt{3}$，$\therefore CF=\frac{AH\cdot CG}{HG}=\frac{3\sqrt{3}CG}{3+DG}$。在$AB$上截取$AN=EC$，连接$EN$。$\because AB=BC$，$\therefore BN=BE$。$\because \angle AEF=\angle ABC=120^{\circ}$，$\angle AEC=\angle AEF+\angle FEC=\angle ABC+\angle BAE$，$\therefore \angle FEC=\angle BAE$。$\because AE=EF$，$\therefore \triangle AEN\cong\triangle EFC$(SAS)，$\therefore CF=EN$。过点$B$作$BM\perp EN$于点$M$。$\because BN=BE$，$\therefore EM=MN$。$\because \angle NBE=120^{\circ}$，$\therefore \angle BEM=30^{\circ}$，$\therefore BE=\frac{1}{\sqrt{3}}EN=\frac{1}{\sqrt{3}}CF$。当$DG=2$，$CG=4$时，$CF=\frac{3\sqrt{3}CG}{3+DG}=\frac{3\sqrt{3}\times4}{3+2}=\frac{12\sqrt{3}}{5}$，$\therefore BE=\frac{1}{\sqrt{3}}CF=\frac{12}{5}$； 当$DG=4$，$CG=2$时，$CF=\frac{3\sqrt{3}CG}{3+DG}=\frac{6\sqrt{3}}{7}$，$\therefore BE=\frac{1}{\sqrt{3}}CF=\frac{6}{7}$。 综上所述，$BE$的长为$\frac{12}{5}$或$\frac{6}{7}$。