《2025年创新思维同步导学案高中数学必修第一册人教版》

[例 2] (1) 函数$y = \lg\frac{1 + x}{1 - x}$的定义域为$(-1,1)$.
(2) 函数$f(x) = \log_{(x + 1)}(16 - 4x)$的定义域为$(-1,0)\cup(0,4)$.

答案： 例2[解析]
(1)由题意得$\frac{1+x}{1-x}＞0$，解得$-1＜x＜1$，
$\therefore$函数的定义域为$(-1,1)$.
(2)要使函数有意义，需满足$\begin{cases}16-4x＞0,\\x+1＞0,\\x+1\neq1,\end{cases}$
解得$-1＜x＜0$或$0＜x＜4$.
$\therefore$函数的定义域为$(-1,0)\cup(0,4)$.
[答案]
(1)$(-1,1)$
(2)$(-1,0)\cup(0,4)$

2. 函数$f(x) = \frac{\sqrt{9 - x^{2}}}{\ln(x + 1)}$的定义域为$(-1,0)\cup(0,3]$.

答案： 跟踪训练
2.解析：由$\begin{cases}x+1＞0,\\x+1\neq1,\\9-x^{2}\geq0,\end{cases}$
解得$-1＜x＜0$或$0＜x\leq3$，
所以函数$f(x)=\frac{\sqrt{9-x^{2}}}{\ln(x+1)}$的定义域为$(-1,0)\cup(0,3]$.
答案：$(-1,0)\cup(0,3]$

[例 3] 为了给地球减负，提高资源利用率，全国掀起了垃圾分类的热潮，垃圾分类已经成为新时尚. 假设某市 2020 年全年用于垃圾分类的资金为 2000 万元，在此基础上，每年的投入资金比上一年增长 20%，则该市全年用于垃圾分类的资金开始超过 1 亿元的年份是(参考数据：$\lg 1.2 ≈ 0.08$，$\lg 5 ≈ 0.70$) (B)

A.2030 年
B.2029 年
C.2028 年
D.2027 年

答案： 例3B[解析] 设经过$n(n\in N^{*})$年后，投入的资金为$y$万元，
则$y=2000(1+20\%)^{n}$.
依题意，$2000(1+20\%)^{n}＞10000$，即$1.2^{n}＞5$，
即$n\lg1.2＞\lg5$，
即$n＞\frac{\lg5}{\lg1.2}\approx\frac{0.7}{0.08}=8.75$，
则$n=9$，所以2029年用于垃圾分类的资金开始超过1亿元.

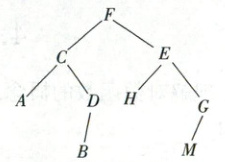
3. 二叉树(Binary tree)是计算机中数据结构的一种，是树形结构的一个重要类型，许多实际问题抽象出来的数据结构往往是二叉树形式. 如图，其中节点是包含一个数据元素及若干指向子树分支的信息，树中所有节点的层次最大值称为树的高度，经实验验证，节点数与树的高度呈指数关系，二叉树的高度$h$与节点数$x$的关系为$x = e^{\frac{h + 4.1}{3.6}}$. 若经测算，一个二叉树的节点大约有 800 个，则二叉树的高度约为($\ln 2 ≈ 0.7$，$\ln 5 ≈ 1.6$，结果保留整数) (D)


A.14
B.16
C.18
D.20

答案： 跟踪训练
3.D解析：$x=e^{\frac{h+4.1}{3.6}}$两边取对数，得$\ln x=\frac{h+4.1}{3.6}$.
将$x=800$代入上式得$h=3.6\ln800-4.1=3.6(5\ln2+2\ln5)-4.1$
$\approx3.6×(5×0.7+2×1.6)-4.1=20.02\approx20$.

1. 已知对数函数的图象过点$M(9, - 2)$，则此对数函数的解析式为 (C)

A.$y = \log_{2}x$
B.$y = \log_{3}x$
C.$y = \log_{\frac{1}{3}}x$
D.$y = \log_{\frac{1}{2}}x$

答案： 随堂测评·自我突破
1.C解析：设函数$f(x)=\log_{a}x(x＞0,a＞0,且a\neq1)$.
$\because$对数函数的图象过点$M(9,-2)$，
$\therefore-2=\log_{a}9$，$\therefore a^{-2}=9$，$a＞0$，解得$a=\frac{1}{3}$
$\therefore$此对数函数的解析式为$y=\log_{\frac{1}{3}}x$.

2. “每天进步一点点”可以用数学来诠释，假如你今天的数学水平是 1，以后每天比前一天增加千分之五，则经过$y$天之后，你的数学水平$x$与$y$之间的函数关系式是 (B)

A.$y = \log_{1.05}x$
B.$y = \log_{1.005}x$
C.$y = \log_{0.95}x$
D.$y = \log_{0.995}x$

答案： 2.B解析：由题意得$x=(1+5‰)^{y}=1.005^{y}$，化为对数函数得$y=\log_{1.005}x$.

3. 若$f(x) = \log_{a}x + (a^{2}-4a - 5)$是对数函数，则$a =$5.

答案： 3.解析：由对数函数的定义可知，$\begin{cases}a^{2}-4a-5=0,\\a＞0,\\a\neq1,\end{cases}$
解得$a=5$.
答案：5

4. 求下列函数的定义域：
(1)$y = \frac{1}{\log_{2}(x - 1)}$；
(2)$y = \log_{2}(16 - 4^{x})$.

答案： 4.解：
(1)要使函数式有意义，需$\begin{cases}x-1＞0,\\\log_{2}(x-1)\neq0,\end{cases}$
解得$x＞1$，且$x\neq2$.
故函数$y=\frac{1}{\log_{2}(x-1)}$的定义域是$\{x|x＞1,且x\neq2\}$.
(2)要使函数式有意义，需$16-4^{x}＞0$，解得$x＜2$.
故函数$y=\log_{2}(16-4^{x})$的定义域是$\{x|x＜2\}$.