《2025年创新思维同步导学案高中数学必修第一册人教版》

3. 在密闭培养环境中，某类细菌的繁殖速度在初期会较快，随着单位体积内细菌数量的增加，繁殖速度又会减慢. 在一次实验中，检测到这类细菌在培养皿中的数量$y$(单位：百万个)与培养时间$x$(单位：小时)的关系为：

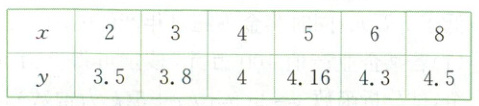
根据表格中的数据画出散点图如下：

为了描述从第 2 小时开始细菌数量随时间变化的关系，现有以下三种模型供选择：
①$y=a \log_{2} x+b$,②$y=a \sqrt{x-3}+b$,③$y=2^{x-a}+b$.
(1)选出你认为最符合实际的函数模型，并说明理由；
(2)利用$(4,4)$和$(8,4.5)$这两组数据求出你选择的函数模型的解析式，并预测从第 2 小时开始，至少再经过多少个小时，细菌数量达到 5 百万个.

答案： 3.解：
(1)依题意，所选函数必须满足三个条件：
a.定义域包含$[2,+\infty)$.
b.增函数.
c.随着自变量的增加，函数值的增长速度变小.
因为函数$y = a\sqrt{x - 3}+b$的定义域为$[3,+\infty)$，$x = 2$时无意义，故不符合实际的函数模型；函数$y = 2^{x - a}+b$随着自变量的增加，函数值的增长速度变大，故不符合实际的函数模型.因为函数$y = a\log_{2}x + b$可以同时符合上述条件，所以应该选择函数$y = a\log_{2}x + b$.
(2)依题意知$\begin{cases} a\log_{2}4 + b=2a + b = 4, \\ a\log_{2}8 + b=3a + b = 4.5, \end{cases}$
解得$\begin{cases} a=\frac{1}{2}, \\ b = 3, \end{cases}$所以$y=\frac{1}{2}\log_{2}x + 3$.
令$y=\frac{1}{2}\log_{2}x + 3\geqslant5$，解得$x\geqslant16$.
所以，至少再经过$14$个小时，细菌数量达到$500$万个.

1. 我国古代著名的思想家庄子在《庄子·天下篇》中说，“一尺之锤，日取其半，万世不竭”. 用现代语言叙述为：一尺长的木棒，每天取其一半，永远也取不完. 这样，每天剩下的部分都是前一天的一半，如果把“一尺之锤”看成单位“1”，那么$x$天后剩下的部分$y$与$x$的函数关系式为 (D)

A.$y=\frac{1}{2}x (x \in \mathbf{N}^*)$
B.$y=x^{\frac{1}{2}} (x \in \mathbf{N}^*)$
C.$y=2^x (x \in \mathbf{N}^*)$
D.$y=\frac{1}{2^x} (x \in \mathbf{N}^*)$

答案： 1.D

2. 某新款电视投放市场后第一个月销售了 100 台，第二个月销售了 200 台，第三个月销售了 400 台，第四个月销售了 790 台，则下列函数模型中，能较好地反映销量$y$与投放市场的月数$x$($1⩽x⩽4,x \in \mathbf{N}^*$)之间关系的是 (C)

A.$y=100x$
B.$y=50x^2 -50x +100$
C.$y=50 × 2^x$
D.$y=100^x$

答案： 2.C 解析：将题目中的数据代入各函数中，易知指数型函数能较好地与题中的数据相对应.

3. 假设某地初始物价为 1，其物价每年以 5％的增长率递增，当该地物价不低于 1.5 时，至少需要经过的年数为(参考数据：取$\lg 2 \approx 0.3, \lg 3 \approx 0.48, \lg 21 \approx 1.32$) (B)

A.8
B.9
C.10
D.11

答案： 3.B 解析：经过$x$年后该地物价为$(\frac{21}{20})^{x}$，
由题意，$(\frac{21}{20})^{x}\geqslant\frac{3}{2}$，
解得$x\geqslant\log_{\frac{21}{20}}\frac{3}{2},\log_{\frac{21}{20}}\frac{3}{2}=\frac{\lg3 - \lg2}{\lg21 - \lg20}$
$\approx\frac{0.48 - 0.3}{1.32 - 0.3 - 1}=9$.

4. 基础建设对社会经济效益产生巨大的作用，某市投入$a$亿元进行基础建设，$t$年后产生$f(t)=a \mathrm{e}^{\frac{t \ln 2}{4}}$亿元社会经济效益，则该市经过12年，该项投资产生的社会经济效益是投资额的 8 倍.

答案： 4.解析：设经过$t$年后，产生的社会经济效益是投资额的$8$倍，则$ae^{\frac{t\ln2}{4}}=8a$，解得$t = 12$.
答案：12