第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 用画图象的方法可以直观地获得结果,但往往难以获得准确的结果.为了获得准确的结果,我们一般用
代数
方法.
答案:
代数
2. 先设出函数表达式,再根据所给条件确定表达式中未知的系数,从而得到函数表达式的方法,叫作
待定系数法
.
答案:
待定系数法
1. 经过两点$(2,3)$,$(-1,-3)$的一次函数的表达式为(
A.$y = x + 1$
B.$y = x - 2$
C.$y = 2x - 1$
D.$y = - 2x + 1$
C
)A.$y = x + 1$
B.$y = x - 2$
C.$y = 2x - 1$
D.$y = - 2x + 1$
答案:
C
2. 国内航空规定,乘坐飞机经济舱旅客所携带行李的重量$x(kg)与其运费y$(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为(
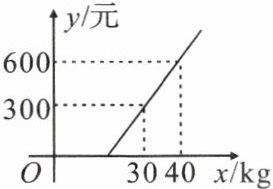
A.$20kg$
B.$25kg$
C.$28kg$
D.$30kg$
A
)
A.$20kg$
B.$25kg$
C.$28kg$
D.$30kg$
答案:
A
3. 在直角坐标系中,一条直线经过$A(-1,5)$,$P(-2,a)$,$B(3,-3)$三点,则$a= $
7
.
答案:
7
4. 小红在练习仰卧起坐,本月$1日至4$日的成绩与日期具有如下关系:
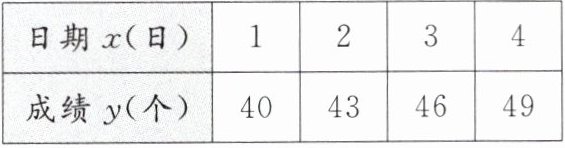
小红的仰卧起坐成绩$y与日期x$之间近似为一次函数关系,则该函数表达式为

小红的仰卧起坐成绩$y与日期x$之间近似为一次函数关系,则该函数表达式为
y=3x+37
.
答案:
y=3x+37
5. (教材第$131页随堂练习第1$题变式)如图,在直角坐标系中,过点$B(6,0)的直线AB与直线OA相交于点A(4,2)$,$C是y$轴上的点.
(1)求直线$AB$的表达式;
(2)求$\triangle OAC$的面积.
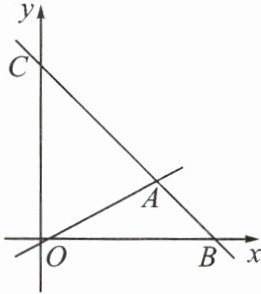
(1)求直线$AB$的表达式;
(2)求$\triangle OAC$的面积.

答案:
(1)解:设直线 AB 的表达式是 y=kx+b,根据题意得{4k+b=2,6k+b=0,解得{k=-1,b=6.则直线 AB 的表达式是 y=-x+6.
(2)在 y=-x+6 中,令 x=0,解得 y=6,
∴C(0,6),
∴S△OAC=1/2×6×4=12.
(1)解:设直线 AB 的表达式是 y=kx+b,根据题意得{4k+b=2,6k+b=0,解得{k=-1,b=6.则直线 AB 的表达式是 y=-x+6.
(2)在 y=-x+6 中,令 x=0,解得 y=6,
∴C(0,6),
∴S△OAC=1/2×6×4=12.
6. (陕西省中考)经验表明,树在一定的成长阶段,其胸径(树的主干在地面以上$1.3m$处的直径)越大,树就越高.通过对某种树进行测量研究,发现这种树的树高$y(m)是其胸径x(m)$的一次函数.已知这种树的胸径为$0.2m$时,树高为$20m$;这种树的胸径为$0.28m$时,树高为$22m$.
(1)求$y与x$之间的函数表达式;
(2)当这种树的胸径为$0.3m$时,其树高是多少?
(1)求$y与x$之间的函数表达式;
(2)当这种树的胸径为$0.3m$时,其树高是多少?
答案:
(1)解:设 y=kx+b(k≠0),由题意得{0.2k+b=20,0.28k+b=22解得{k=25,b=15,
∴y与 x 之间的函数表达式为 y=25x+15.
(2)当 x=0.3m 时,y=25×0.3+15=22.5(m).
∴当这种树的胸径为 0.3m 时,其树高为 22.5m.
(1)解:设 y=kx+b(k≠0),由题意得{0.2k+b=20,0.28k+b=22解得{k=25,b=15,
∴y与 x 之间的函数表达式为 y=25x+15.
(2)当 x=0.3m 时,y=25×0.3+15=22.5(m).
∴当这种树的胸径为 0.3m 时,其树高为 22.5m.
7. 对于一次函数$y = kx + b$,当$1\leqslant x\leqslant 4$时,$3\leqslant y\leqslant 6$,则一次函数的表达式为
y=x+2 或 y=-x+7
.
答案:
y=x+2 或 y=-x+7
查看更多完整答案,请扫码查看


