第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
10. 已知$m= \sqrt{4}+\sqrt{3}$,则以下对$m$的估算正确的是(
A.$2<m<3$
B.$3<m<4$
C.$4<m<5$
D.$5<m<6$
B
)A.$2<m<3$
B.$3<m<4$
C.$4<m<5$
D.$5<m<6$
答案:
B
11. (资阳市中考)若$a= \sqrt[3]{7}$,$b= \sqrt{5}$,$c = 2$,则$a$,$b$,$c$的大小关系为(
A.$b<c<a$
B.$b<a<c$
C.$a<c<b$
D.$a<b<c$
C
)A.$b<c<a$
B.$b<a<c$
C.$a<c<b$
D.$a<b<c$
答案:
C
12. 利用计算器进行如下操作:$SHIFT$ $\sqrt{\blacksquare}$ 1 7 8 $=$,屏幕显示的结果为5.625,那么进行如下操作:$SHIFT$ $\sqrt{\blacksquare}$ 0 $·$ 1 7 8 $=$,那么屏幕显示的结果为
0.5625
。
答案:
0.5625
13. (1)用计算器计算:
①$\sqrt{121}=$
②$\sqrt{12321}=$
③$\sqrt{1234321}=$
④$\sqrt{123454321}=$
……
猜想:$\sqrt{1212345678987654321}=$
(2)用计算器计算:
①$\sqrt{9×9 + 19}=$
②$\sqrt{99×99 + 199}=$
③$\sqrt{999×999 + 1999}=$
……
猜想:$\sqrt{\underset{n个9}{\underbrace{99…9}}×\underset{n个9}{\underbrace{99…9}}+\underset{n个9}{\underbrace{199…9}}}=$
①$\sqrt{121}=$
11
;②$\sqrt{12321}=$
111
;③$\sqrt{1234321}=$
1111
;④$\sqrt{123454321}=$
11111
;……
猜想:$\sqrt{1212345678987654321}=$
111111111
。(2)用计算器计算:
①$\sqrt{9×9 + 19}=$
10
;②$\sqrt{99×99 + 199}=$
100
;③$\sqrt{999×999 + 1999}=$
1000
;……
猜想:$\sqrt{\underset{n个9}{\underbrace{99…9}}×\underset{n个9}{\underbrace{99…9}}+\underset{n个9}{\underbrace{199…9}}}=$
$10^{n}$
。
答案:
(1)①11 ②111 ③1111 ④11111 111111111
(2)①10 ②100 ③1000 $10^{n}$
(1)①11 ②111 ③1111 ④11111 111111111
(2)①10 ②100 ③1000 $10^{n}$
14. (新考法)(1)下面是小李探索$\sqrt{2}$的近似值的过程,请补充完整:
我们知道面积是2的正方形的边长是$\sqrt{2}$,且$\sqrt{2}>1$。设$\sqrt{2}= 1 + x$,可画出如下示意图。
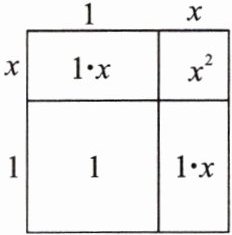
由面积公式,可得$x^{2}+$____$=2$,略去$x^{2}$,得方程____。解得$x= $____。即$\sqrt{2}\approx$____。
(2)仿照上述方法,利用(1)的结论,再探究一次,使求得的$\sqrt{2}$的近似值更加准确。
(画出示意图,标明数据,并写出求解过程)
我们知道面积是2的正方形的边长是$\sqrt{2}$,且$\sqrt{2}>1$。设$\sqrt{2}= 1 + x$,可画出如下示意图。

由面积公式,可得$x^{2}+$____$=2$,略去$x^{2}$,得方程____。解得$x= $____。即$\sqrt{2}\approx$____。
(2)仿照上述方法,利用(1)的结论,再探究一次,使求得的$\sqrt{2}$的近似值更加准确。
(画出示意图,标明数据,并写出求解过程)
答案:
(1)$2x + 1$ $2x + 1 = 2$ 0.5 1.5
(2)解:因为$x^{2} > 0$,所以$2x + 1 < 2$,所以$x < 0.5$,所以$\sqrt{2} < 1.5$.所以设$\sqrt{2} = 1.5 - x$,示意图如图所示 .由面积公式,可得$x^{2} + 2x(1.5 - x) + 2 = 1.5^{2}$,整理,得$-x^{2} + 3x + 2 = 2.25$,略去$x^{2}$,得方程$3x + 2 = 2.25$,解得$x = 0.0833…$,即$\sqrt{2} \approx 1.4167$.
.由面积公式,可得$x^{2} + 2x(1.5 - x) + 2 = 1.5^{2}$,整理,得$-x^{2} + 3x + 2 = 2.25$,略去$x^{2}$,得方程$3x + 2 = 2.25$,解得$x = 0.0833…$,即$\sqrt{2} \approx 1.4167$.
(1)$2x + 1$ $2x + 1 = 2$ 0.5 1.5
(2)解:因为$x^{2} > 0$,所以$2x + 1 < 2$,所以$x < 0.5$,所以$\sqrt{2} < 1.5$.所以设$\sqrt{2} = 1.5 - x$,示意图如图所示
 .由面积公式,可得$x^{2} + 2x(1.5 - x) + 2 = 1.5^{2}$,整理,得$-x^{2} + 3x + 2 = 2.25$,略去$x^{2}$,得方程$3x + 2 = 2.25$,解得$x = 0.0833…$,即$\sqrt{2} \approx 1.4167$.
.由面积公式,可得$x^{2} + 2x(1.5 - x) + 2 = 1.5^{2}$,整理,得$-x^{2} + 3x + 2 = 2.25$,略去$x^{2}$,得方程$3x + 2 = 2.25$,解得$x = 0.0833…$,即$\sqrt{2} \approx 1.4167$. 查看更多完整答案,请扫码查看


