第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
8. 如图,小颖从家到学校要穿过一个居民小区,小区的道路是正南或正东方向的. 小颖走下面的路线不能到达学校的是(
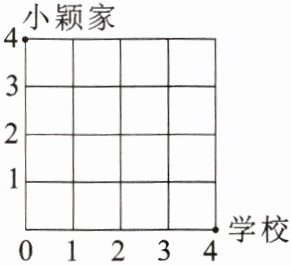
A.$(0,4)→(0,0)→(4,0)$
B.$(0,4)→(4,4)→(4,0)$
C.$(0,4)→(1,4)→(1,1)→(4,1)→(4,0)$
D.$(0,4)→(3,4)→(4,2)→(4,0)$
D
)
A.$(0,4)→(0,0)→(4,0)$
B.$(0,4)→(4,4)→(4,0)$
C.$(0,4)→(1,4)→(1,1)→(4,1)→(4,0)$
D.$(0,4)→(3,4)→(4,2)→(4,0)$
答案:
D
9. (甘肃省中考)敦煌文书是华夏民族引以为傲的艺术瑰宝,其中敦煌《算经》中出现的《田积表》部分如图 1 所示,它以表格形式将矩形土地的面积直观展示,可迅速准确地查出边长 10 步到 60 步的矩形田地面积,极大地提高了农田面积的测量效率. 如图 2 是复原的部分《田积表》,表中对田地的长和宽都用步来表示,A 区域表示的是长 15 步,宽 16 步的田地面积为一亩,用有序数对记为$(15,16)$,那么有序数对记为$(12,17)$对应的田地面积为(

A.一亩八十步
B.一亩二十步
C.半亩七十八步
D.半亩八十四步
D
)
A.一亩八十步
B.一亩二十步
C.半亩七十八步
D.半亩八十四步
答案:
D
10. (新情境)两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚—咚咚,咚—咚,咚咚咚—咚”表示的动物是“狗”,则听到“咚咚—咚,咚咚咚—咚咚,咚—咚咚咚”时,表示的动物是
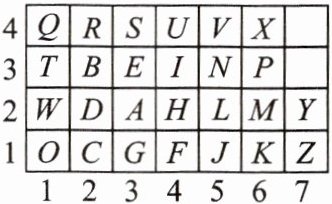
猫
.
答案:
猫
11. 如图,小丽以学校为观测点,画了一张平面图.
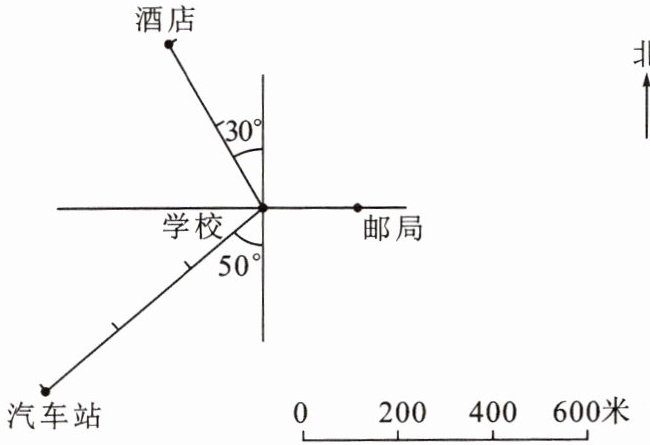
(1)由图知酒店在学校____偏____ ____方向____米处,汽车站在学校____偏____ ____方向____米处;
(2)医院在邮局东偏北$60^{\circ}$方向 400 米处,请在图中标出它的位置;
(3)小丽以每分钟 50 米的速度步行,从汽车站经过学校、邮局再到医院,大约需要____分钟.

(1)由图知酒店在学校____偏____ ____方向____米处,汽车站在学校____偏____ ____方向____米处;
(2)医院在邮局东偏北$60^{\circ}$方向 400 米处,请在图中标出它的位置;
(3)小丽以每分钟 50 米的速度步行,从汽车站经过学校、邮局再到医院,大约需要____分钟.
答案:
(1)北 西 30° 400 南 西 50° 600
(2)解:如图所示

(3)24
(1)北 西 30° 400 南 西 50° 600
(2)解:如图所示

(3)24
12. (核心素养·应用意识)如图,一艘轮船先从 A 地出发行驶到 B 地,又从 B 地行驶到 C 地,已知 B 地在 A 地南偏西$40^{\circ}$的方向,距离 A 地 80 海里,C 地在 B 地北偏西$50^{\circ}$的方向,距离 B 地 100 海里.
(1)表示出 B 地相对于 C 地的位置;
(2)求 A,C 两地之间的距离.
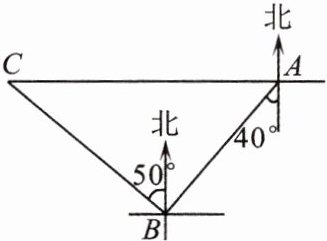
(1)表示出 B 地相对于 C 地的位置;
(2)求 A,C 两地之间的距离.

答案:
(1)解:B地位于C地的南偏东50°方向,距离C地100海里.
(2)由行驶的方向可得:∠ABC=90°,在Rt△ABC中,由勾股定理可得AC = $\sqrt{AB²+BC²}$=20 $\sqrt{41}$(海里).
(1)解:B地位于C地的南偏东50°方向,距离C地100海里.
(2)由行驶的方向可得:∠ABC=90°,在Rt△ABC中,由勾股定理可得AC = $\sqrt{AB²+BC²}$=20 $\sqrt{41}$(海里).
查看更多完整答案,请扫码查看


