《2025年课堂点睛八年级数学上册北师大版》

1. 整数和分数统称为有理数. 它们都可以用有限小数或无限循环小数来表示.

答案： 有理数　循环

2. 在等式 $ a^{2}= 2 $ 中,$ a $ 既不是整数,也不是分数,所以 $ a $ 不是有理数.

答案： 整数　有理数

1. 已知在 $ \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ AC = 4 $,$ BC = 5 $,那么斜边 $ AB $ 的长是 (D)
A.整数
B.分数
C.有理数
D.非有理数

答案： D

2. 如图,每个小正方形的边长为 1,则 $ \triangle ABC $ 中,边长不是有理数的个数是 (C)

A.0 个
B.1 个
C.2 个
D.3 个

答案： C

3. 已知一个圆的面积为 $ 9\pi $,则其半径 $ r $是(选填“是”或“不是”)有理数.

答案： 是

4. 一个长方形的长是 2,宽是 1,它的对角线长的平方是5,对角线长不是(选填“是”或“不是”)有理数.

答案： 5　不是

5. 面积分别为 1,2,3,4,5,6 的正方形,其中边长是有理数的正方形有2个,边长不是有理数的正方形有4个.

答案： 2　4

6. 下列字母表示的数中,不是有理数的有①④(填序号).
①体积为 9 的正方体的棱长 $ a $；②三角形的面积为 4,一条边长为 3,其边上的高 $ h $；③ $ a = 0.\dot{3}\dot{7} $；④直角三角形两直角边长为 2,4,其斜边长 $ c $.

答案： ①④

7. 已知一个表面积为 36 的正方体,则这个正方体的棱长不是有理数(选填“是”或“不是”).

答案： 不是

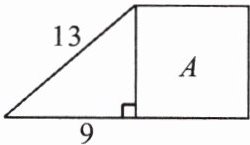
8. 如图,正方形 $ A $ 的面积是88,这个正方形的边长不是(选填“是”或“不是”)有理数.

答案： 88　不是

9.(教材第 26 页随堂练习第 1 题变式)如图,正三角形 $ ABC $ 的边长为 4,高为 $ h $. $ h $ 是分数吗？是整数吗？是有理数吗？说明理由.

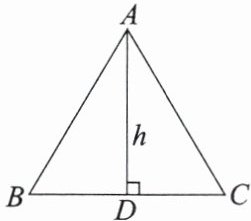
答案： 解:都不是.理由:由题意可知AB=4,BD=2.在Rt△ABD中,$h^{2}=AB^{2}-BD^{2}=4^{2}-2^{2}=12$,所以h不是分数，也不是整数，也不是有理数.

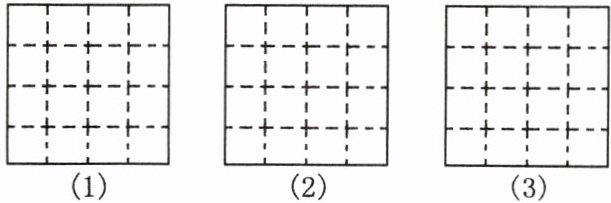
10.(核心素养·创新意识)请按如下要求设计直角三角形.
(1)使它的三边中有一边边长不是有理数；
(2)使它的三边中有两边边长不是有理数；
(3)使它的三边边长都是有理数.

答案：
解:如图所示　　 (画法不唯一)